Компьютерная алгебра в программе Mathematica 4
С действием других функций нетрудно
Пример 11.10.
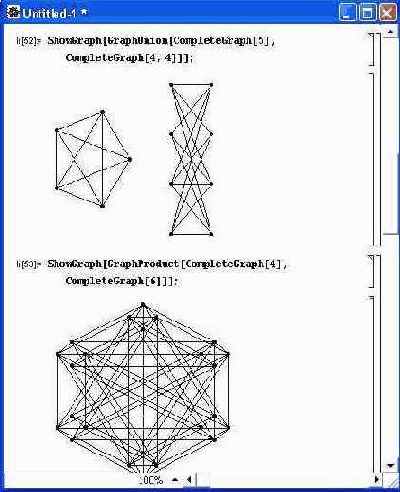
Создание графов с помощью функций GraphUnion и GraphProduct С действием других функций нетрудно ознакомиться самостоятельно.
|
Свойства графов
|
||
|
ArticulationVertices
|
Automorphisms
|
Bi Connected Components |
|
BiconnectedQ
|
BipartiteQ
|
Bridges
|
|
ChromaticNumber
|
Chromatic Polynomial |
CliqueQ
|
|
Connected Components |
ConnectedQ
|
DeBruijnSequence
|
|
DeleteCycle
|
EdgeChromatic Number |
EdgeColoring
|
|
EdgeConnectivity
|
Element
|
EulerianCycle
|
|
EulerianQ
|
ExtractCycles
|
FindCycle
|
|
Girth
|
GraphPower
|
HamiltonianCycle
|
|
HamiltonianQ
|
Harary
|
HasseDiagram
|
|
IdenticalQ
|
Independent SetQ
|
IsomorphicQ
|
|
Isomorphism
|
IsomorphismQ
|
MaximumClique
|
|
Maximum lndependentSet |
Minimum VertexCover |
OrientGraph
|
|
PartialOrderQ
|
PerfectQ
|
SelfComplementaryQ
|
|
StronglyConnected Components |
TopologicalSort
|
TransitiveClosure
|
|
TransitiveReduction
|
TravelingSalesman
|
TravelingSalesman Bounds |
|
TreeQ
|
Trianglelnequality
|
TwoColoring
|
|
VertexColoring
|
VertexConnectivity
|
VertexCoverQ
|
|
WeaklyConnected Components |
||