Компьютерная алгебра в программе Mathematica 4
Визуализация решения квадратного уравнения для случая двух действительных корней
Пример 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней
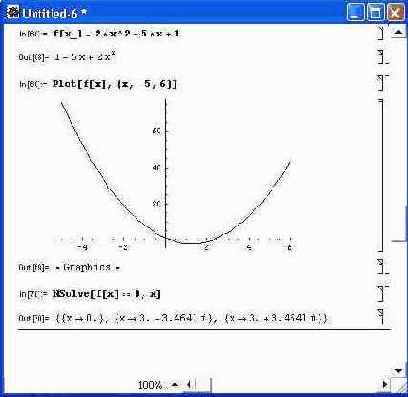
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы. Если требуется решение равенства f1(х) = f 2 (x), то для графической визуализации решения можно построить графики функций f1(х) и f 2 (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.