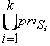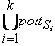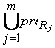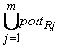Алгоритм обхода ndfsm
Основная идея алгоритма обхода ndfsm заключается в следующем. Если в недетерминированном графе существует детерминированный сильносвязный полный остовный подграф, то алгоритм движения может использовать этот подграф для построения обхода, не сталкиваясь непосредственно с проблемами недетерминизма.
Ориентированный граф G' = ( VG', XG', EG' ) называется остовным подграфом ориентированного графа G = ( VG, XG, EG ), если VG' = VG, XG' = XG и EG'

Остовный подграф G' = ( VG', XG', EG' ) ориентированного графа G = ( VG, XG, EG ) называется полным остовным подграфом, если






Напомним, что алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v



Пусть e = ( e1, e2, …, en ) - пройденный маршрут в графе G = ( VG, XG, EG ). Тогда мы будем использовать следующие обозначения. Множеством пройденных вершин VGe мы будем называть множество вершин пройденного маршрута:
VGe = { vg




Пройденным подграфом мы будем называть граф G'e = ( VGe, XG, { e1, e2, …, en } ).
Пусть ei = ( vi, xgi, v'i ). Тогда детерминированным пройденным подграфом мы будем называть граф G''e = ( VGe, XG, { ei |




Будем говорить, что стимул xg пройден в вершине vg, если существуют такая вершина vg'


Если в вершине vg все допустимые стимулы являются пройденными, то такая вершина будет называться завершенной.
Для обеспечения детерминированности функции мы будем считать, что множество стимулов XG является фундированным, то есть множество линейно упорядоченно и в нем отсутствует бесконечно убывающая последовательность элементов.
Определение 20.
Алгоритмом движения ndfsm мы будем называть функцию αndfsm, которая по неизбыточному описанию ориентированного графа G = ( VG, XG, π ), текущей вершине v



Если текущая вершина не является завершенной, то функция возвращает минимальный стимул из π(v), который не является пройденным в текущей вершине; Иначе, если в детерминированном пройденном подграфе существует маршрут, ведущий из текущей вершины в какую-либо из незавершенных пройденных вершин, то функция возвращает стимул, приписанный к дуге ei пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин; В противном случае функция возвращает τ.
Корректность определения следует из фундированности множества стимулов и конечности пройденного подграфа.
При работе с недетерминированными графами алгоритм движения не может гарантировать обход всех дуг графа, так как алгоритм не может выбрать конкретную дугу среди набора дуг, начинающихся в одной вершине и помеченных одним стимулом. Этот выбор происходит недетерминированно и независимо от работы алгоритма движения. Поэтому для недетерминированных графов вводится понятие обхода по стимулам, которое совпадает с понятием обхода на классе детерминированных графов и является более слабым на классе недетерминированных графов.
Обходом по стимулам [] конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1
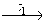
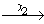
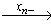


Алгоритм движения α называется алгоритмом обхода по стимулам на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом по стимулам графа G.
Лемма.
Алгоритм движения ndfsm является алгоритмом обхода по стимулам на классе конечных графов, обладающих детерминированным сильносвязным полным остовным подграфом.
Доказательство.
Предположим, что это не так. Тогда существует конечный граф G = ( VG, XG, EG ), обладающий детерминированным сильносвязным полным остовным подграфом, и функционирование e = ( e1, e2, …, en, … ) алгоритма ndfsm на этом графе такие, что e не является конечным обходом по стимулам графа G. Такое может быть в двух случаях: если функционирование e является конечным, но не является обходом по стимулам графа G, и если функционирование e является бесконечным.
1. Предположим, что функционирование e = ( e1, e2, …, en ) является конечным, но не является обходом по стимулам графа G. Тогда из определения функционирования следует, что αndfsm( A, v'n, e ) = τ . Следовательно вершина v'n является завершенной и в детерминированном пройденном подграфе G''e не существует маршрута, ведущего из вершины v'n в какую-либо из незавершенных пройденных вершин.
С другой стороны e не является обходом по стимулам графа G, то есть в графе G существует такая дуга ( v, x, v' )


Рассмотрим детерминированный сильносвязный полный остовный подграф G' = ( VG', XG', EG' ) графа G. Так как подграф является остовным, то обе вершины v и v'n принадлежат VG'. Так как граф G конечный, а его подграф G' - сильносвязный, то существует конечный маршрут f = ( f1, f2, …, fk ), ведущий из v'n в v. Пусть fi = ( wi, yi, w'i ). Тогда для всех i



Следовательно, наше предположение относительно существования второй дуги ( wi, yi, w''i )

Докажем индукцией по пути f = ( f1, f2, …, fk ), что все вершины w'i являются завершенными для i

База индукции . Вершина w1 = v'n

Предположение индукции . Пусть вершина w'i-1 = wi является завершенной.
Шаг индукции . Так как вершина wi является завершенной, стимул yi является допустимым в этой вершине и дуга ( wi, yi, w'i ) является единственной дугой, выходящей из wi и помеченной стимулом yi, то дуга ( wi, yi, w'i ) также является пройденной, то есть ( wi, yi, w'i )

Мы доказали, что все вершины w'i являются завершенными. Следовательно, и вершина w'k = v

2. Предположим, что функционирование e = ( e1, e2, …, en, … ) является бесконечным. Тогда для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ.
Определим функцию βG на графе G, устанавливающую соответствие между маршрутом ( e1, …, ei ) в графе G и парой натуральных чисел (b1,b2), следующим образом:
b1 равно числу дуг графа G, отсутствующих в маршруте ( e1, …, ei ), |EG \ { e1, …, ei }|; b2 равно
0, если i = 0, вершина v'i является незавершенной или в детерминированном пройденном подграфе нет маршрута, ведущего из вершины v'i и в какую-либо из незавершенных пройденных вершин; минимальной длине маршрута в детерминированном пройденном подграфе, начинающегося в вершине v'i и заканчивающегося в какой-либо из незавершенных пройденных вершин, в противном случае.
Определим на множестве пар натуральных чисел линейный порядок:
(b1,b2) < (b'1,b'2)



Отметим, что множество пар натуральных чисел с данным линейным порядком образуют фундированное множество, то есть множество, в котором отсутствует бесконечно убывающая последовательность элементов.
Согласно определению βG( () ) = (|EG|,0).
Покажем, что для любого префикса ( e1, …, ei ) функционирования e
βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) )
Для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ. Следовательно, либо вершина v'i не является завершенной, либо в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин.
Рассмотрим первый случай. Если вершина v'i не является завершенной, то αndfsm возвращает минимальный стимул из π(v), который не является пройденным в вершине v'i. На этом основании можно сделать вывод, что ei+1 является дугой, не принадлежащей { e1, …, ei }. Поэтому первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), откуда следует, что βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Рассмотрим второй случай. Если вершина v'i является завершенной и в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин, то αndfsm возвращает стимул, приписанный к дуге ej пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин.
При этом дуга ei+1 может либо совпасть c дугой ej, либо нет.
Если дуга ei+1 совпадает c дугой ej, то уменьшается на единицу второй компонент функции βG, так как кратчайший маршрут в детерминированном пройденном подграфе станет на одну дугу короче, или же в результате перехода будет достигнута незавершенная вершина. При этом первая компонента функции βG останется неизменной, поэтому βG( ( e1, …, ei, ei+1 ) ) будет меньше βG( ( e1, …, ei ) ).
Если дуга ei+1 не совпадает c дугой ej, то эта дуга не принадлежит { e1, …, ei }, так как в противном случае дуга ej не была бы частью детерминированного пройденного подграфа. Следовательно первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), то есть βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Мы показали, что для всех i ≥ 0 βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ). Следовательно функционирование e не может быть бесконечным, так как в противном случае последовательность βG( ( e1, …, ei ) ) образует бесконечно убывающую подпоследовательность в фундированном множестве.
Алгоритм движения ndfsm позволяет заменять стандартный алгоритм dfsm, в тех случаях когда отдельные сценарные функции имеют недетерминированную природу, а другие гарантировано обеспечивают детерминированное движение по графу.
Определение 21.
Асинхронным тестовым сценарием ndfsm относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с множеством стабильных состояний VS


Алгоритм проверки корректности поведения
Предположим, что нам даны конечная асинхронная модель поведения целевой системы ( P,


Для этого необходимо проверить существование пути ( e1, e2, …, en ) в автомате A, начинающегося в состоянии v0 и помеченного взаимодействиями из P так, чтобы это не противоречило частичному порядку π.
Асинхронная модель требований A = ( V, X, Y, Z, E ) задается асинхронной спецификацией { SpecSi | i = 1, …, k; k > 0 }

В данном разделе мы не будем рассматривать пути решения этой проблемы. Здесь мы будем считать, что нам задана вспомогательная функция γ : V x ( (X x Y)


γ( v, p ) = { v'


Но даже в этом случае для проверки корректности поведения требуется рассмотреть все возможные линеаризации асинхронной модели поведения и для каждой из них проверить существование соответствующего пути в автомате A.
Определение 12.
Линейный порядок < на частично-упорядоченном множестве ( P,






Для последующего рассмотрения введем вспомогательную функцию Г*, вычисляющую по состоянию в автомате и последовательности асинхронных взаимодействий, множество состояний автомата, достижимых из данного по последовательности дуг, помеченных данной последовательностью взаимодействий.
Формальное определение функции Г* следующее:
Г* ( v0, ( p1, p2, …, pn ) ) =

Г( V, p ) =
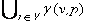
Лемма.
Для последовательности асинхронных взаимодействий ( p1, p2, …, pn ) существует путь ( e1, e2, …, en ) в автомате A, начинающийся в состоянии v0 и помеченный данными взаимодействиями, тогда и только тогда, когда Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Доказательство.
Действительно, пусть существует путь v0
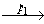
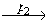
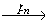

Базис индукции. (n = 1)
Итак, пусть v0
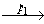



Шаг индукции.
Предположим, что мы доказали утверждение для путей длины n-1. Докажем его для n.
Пусть существует путь v0





В обратную сторону.
Пусть Г*( v0, ( p1, p2, …, pn ) ) ≠ Ø. Докажем индукцией по n, что в автомате A существует путь v0
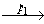
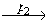
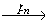
Базис индукции. (n = 1)
Пусть Г* ( v0, ( p1 ) ) ≠ Ø. Тогда существует v1

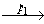
Шаг индукции.
Предположим, что мы доказали утверждение для n-1. Докажем его для n.
Пусть Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Тогда




Предположим, что это не так.
То есть




Тогда Г* ( v0, ( p1, p2, …, pn ) ) = Г( … Г( Г* ( v0, ( p1, p2, …, pk ) ), pk+1 ), … pn ) =
=
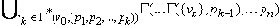
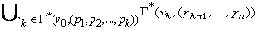
=
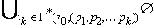
Данное утверждение верно и для k = 1. То есть найдется такое состояние v1

Так как v1

Как следует из леммы, проверка существования пути в автомате сводится к последовательному применению функции Г, вычислительная сложность которого сильно зависит от числа состояний, допускаемых моделью требований в качестве постсостояния перехода с заданными пресостоянием и асинхронным взаимодействием. В дальнейших оценках мы будем считать, что асинхронная модель требований допускает не более одного такого состояния, то есть модель является детерминированной.
Асинхронная модель требований A = ( V, X, Y, Z, E ) называется детерминированной, если для каждого состояния v





Для детерминированных моделей проверка существования пути, начинающегося в заданном состоянии v0 и помеченного заданной последовательностью взаимодействий ( p1, p2, …, pn ), в худшем случае сводится к n-кратному вычислению функции γ. Таким образом, сложность этой проверки оценивается сверху n-кратной сложностью вычисления функции γ.
Для оценки корректности асинхронной модели поведения такую проверку необходимо выполнить для каждой возможной линеаризации мультимножества асинхронных взаимодействий. А в худшем случае число линеаризаций составляет n!, где n - мощность множества P. То есть общая оценка сложности составляет n · n!.
Заметим, что многие линеаризации имеют общее начало. Этим свойством можно воспользоваться, чтобы не дублировать проверку существования путей, соответствующих общему началу линеаризаций.
Определим для множества P дерево возможных линеаризаций, как дерево, в котором
из корня выходит n дуг, из вершин первого уровня - n-1 дуга, …, из вершин n-го уровня - 1 дуга и из вершин n+1-го уровня - ни одной дуги. каждая дуга помечена элементом из P, дуги, выходящие из вершины, путь к которой из корня дерева помечен последовательностью ( p1, p2, …, pk ), помечены элементами P, которые составляют множество Р \ { p1, p2, …, pk }.
Пример дерева возможных линеаризаций для P = { 1, 2, 3 } представлен на рисунке 11.
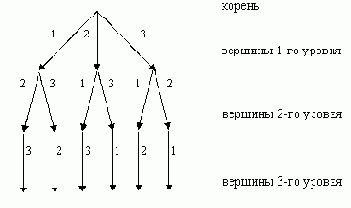
Рисунок 11. Дерево возможных линеаризаций для Р = { 1, 2, 3 }.
Заметим, что пути, ведущие из корня в листья, помечены последовательностями элементов из P, каждая из которых является линеаризацией множества P, а все вместе они образуют множество всех возможных линеаризаций.
Припишем к каждой вершине дерева возможных линеаризаций подмножество P, составленное из элементов { p1, p2, …, pk }, которыми помечен путь из корня дерева к данной вершине.
Деревом возможных линеаризаций частично-упорядоченного множества ( P,


Идеалами частично-упорядоченного множества ( P,






Лемма.
Пути из корня в листья дерева возможных линеаризаций частично-упорядоченного множества ( P,


Доказательство.
Покажем, что любой путь из корня в лист помечен последовательностью являющейся линеаризаций. Действительно, по построению дерева, любая такая последовательность является упорядочиванием всех элементов P. Покажем, что определяемый ею линейный порядок сохраняет исходный частичный порядок

Предположим, что это не так. То есть




Из того, что p2 < p1 следует, что дуга, помеченная p2, встречается в пути раньше, чем дуга, помеченная p1. Следовательно, к вершине, в которую ведет дуга, помеченная p2, приписано множество, содержащее p2 и не содержащее p1. Такое множество не является идеалом, то есть рассматриваемые дуги не могут принадлежать дереву возможных линеаризаций. Противоречие показывает, что наше предположение не верно и любая последовательность на пути из корня в лист является линеаризаций.
Докажем, что для любой линеаризации ( P,

Для этого мы рассмотрим путь в дереве возможных линеаризаций множества P, помеченный соответствующей последовательностью элементов ( p1, p2, …, pn ), и покажем, что этот путь будет присутствовать в дереве возможных линеаризаций частично-упорядоченного множества ( P,

Предположим, что это не так и одна из вершин этого пути была удалена из дерева. Это могло произойти только в случае, когда данная вершина принадлежит поддереву, к корню которого приписано множество, не являющееся идеалом ( P,


Это множество состоит из элементов, приписанных к пути из корня дерева в эту вершину. Так как такой путь в дереве единственен, то он совпадает с началом пути ( p1, p2, …, pn ). Следовательно,


То есть существуют такие i и j, что pi





Отсюда, i ≤ k < j


Если не дублировать проверку существования путей, соответствующих общему началу линеаризаций, то число необходимых вычислений функции γ будет совпадать с числом дуг в дереве возможных линеаризаций. Число дуг в дереве для множества размерностью n составляет:
n + n·(n-1) + … + n·(n-1)· … ·1 =
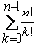
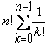
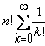
Основной сложностью в реализации этого алгоритма является организация перебора возможных линеаризаций асинхронной модели поведения ( P,

С другой стороны, существуют другие алгоритмы перебора перестановок, которые позволяют сократить затраты на проверку того, является ли очередная перестановка линеаризацией или нет. Но применение нетривиального перебора линеаризаций должно обеспечивать не только сложность O(n!), но и избегать перебора k! заведомо неподходящих перестановок, в тех случаях, когда известно, что (n-k)-ый элемент в какой-то перестановке нарушает условия линеаризации.
Алгоритм перебора линеаризаций, удовлетворяющий всем этим требованиям, был построен на основе алгоритма перебора перестановок 1.11, описанного в []. Этот алгоритм обеспечивает перебор перестановок таким образом, что каждая последующая перестановка отличается от предыдущей транспозицией одной пары элементов. В результате, проверка соответствия очередной перестановки условиям линеаризации требует в большинстве случаев константного времени. И в то же время, данный алгоритм позволяет избежать перебора k! заведомо неподходящих перестановок.
Алгоритм проверки корректности поведения, представленный ниже, основан на обходе дерева возможных линеаризаций в глубину. В нем используется следующая вспомогательная функция int B (int m , int i ), сложность вычисления которой ограничена константой:
int B(int m, int i) { if ((m%2 == 0) && (m > 2)) {if ( i < m-1 )
return i; else return m-2; }
else return m-1; }
Сам алгоритм представлен далее.
Алгоритм проверки корректности поведения.
Входные данные.
Асинхронная модель поведения ( P,

массивом асинхронных взаимодействий P ( |P| = n ); двухмерным массивом частичного порядка order[n,n] order[i,j] = 1, если P[i]

Асинхронная модель требований A = ( V, X, Y, Z, E ) задана функцией возможных постсостояний γ : V x ( (X x Y)


Начальное состояние v0

Данные алгоритма.
bound : Nat[n] := { n, n-1, …, 2, 1 }
массив счетчиков числа точек ветвления дерева возможных линеаризаций.
perm : Nat[n] := { 0, 1, …, n-1 }
массив, хранящий текущую перестановку взаимодействий.
current : Nat := 0
индекс текущего элемента перестановки.
path : (V-set)[n+1] := { {v0}, Ø, …, Ø }
массив множеств состояний текущего пути в модели требований. Для детерминированных моделей требований этот массив может быть заменен на массив состояний V, так как все его элементы будут множествами с размерностью не более 1.
processed : Nat := 0
индекс наибольшего элемента пути, содержащего актуальное множество состояний модели требований.
order_failed : Bool := false
флаг, содержащий истинное значение только в том случае, когда текущая перестановка не является линеаризацией частичного порядка

current2 : Nat := 0
вспомогательная переменная для хранения индекса второго взаимодействий, участвовавшего в последней транспозиции.
tmp : Nat := 0
вспомогательная переменная.
j : Nat := 0
вспомогательная переменная.
Алгоритм.
Алгоритм вычисляет является ли текущая перестановка perm линеаризацией частичного порядка



for(;current<n-1;current++) {for(j=current+1;j<n;j++) {if (order[perm[j],perm[current]]) {order_failed = true; goto 3; } } }
order_failed = false;
Алгоритм строит пути в модели требований, соответствующие последовательности взаимодействий в текущей перестановке, заполняя массив path. При этом предполагается, что начальные отрезки пути path[0], …, path[processed] уже построены ранее. Если на одном из шагов множество состояний модели требований оказывается пустым, то алгоритм переходит к шагу problem, установив значение переменной current равное индексу элемента перестановки для которого было получено пустое множество. Если же path[n] ≠ Ø, то алгоритм завершает свою работу с положительным вердиктом. Найдена линеаризация ( P[perm[0]], P[perm[1]],…, P[perm[n-1]] ), для которой множество Г*( v0, ( P[perm[0]], P[perm[1]], …, P[perm[n-1]] ) ) = path[n] не пусто.
for(;processed<n;processed++) {path[processed+1] = Ø; foreach v : V in path[processed] path[processed+1] = path[processed+1]

КОНЕЦ ( асинхронная модель поведения является корректной относительно данной асинхронной модели требований)
Если индекс текущего элемента перестановки больше либо равен n-2 или , то алгоритм переходит к шагу 9.
if ((current ≥ n-2) || (bound[current] == 1)) goto 9;
Если индекс текущего элемента перестановки является нечетным при обратной нумерации элементов перестановки [n-1


if ((n-current) % 2 == 0) goto 7;
Алгоритм осуществляет циклический сдвиг хвоста перестановки на единицу
perm[current+2]



tmp = perm[current+1]; for(j=current+1;j<n-1;j++) perm[j] = perm[j+1]; perm[n-1] = tmp;
Если предыдущая перестановка не противоречила частичному порядку

if (!order_failed) {for(j=current+1;j<n-1;j++) {if (order[perm[n-1],perm[j]]) {order_failed = true; break; } } }
goto 9;
Алгоритм осуществляет транспозицию элементов перестановки с индексами current+1 и current+2.
tmp = perm[current+1]; perm[current+1] = perm[current+2]; perm[current+2] = tmp;
Если предыдущая перестановка не противоречила частичному порядку

if (!order_failed) {if (order[perm[current+2],perm[current+1]]) order_failed = true; }
Если текущий счетчик числа точек ветвления равен 1, то алгоритм переходит к шагу 14.
if (bound[current] == 1) goto 14;
Алгоритм осуществляет транспозицию элементов перестановки с индексами current и n-B(n-current,n-current-bound[current]+1), сохраняя индекс второго элемента в переменной current2.
current2 = n-B(n-current,n-current-bound[current]+1); tmp = perm[current]; perm[current] = perm[current2]; perm[current2] = tmp;
Алгоритм уменьшает текущий счетчик числа точек ветвления на единицу.
bound[current]--;
Если предыдущая перестановка противоречила частичному порядку

if (order_failed) goto 1;
В противном случае алгоритм вычисляет, не противоречит ли новая перестановка частичному порядку


for(j=current+1;j<=current2;j++) {if (order[perm[j],perm[current]]) {order_failed = true; goto 3; } }
for(j=current+1;j<current2;j++) {if (order[perm[current2],perm[j]]) {order_failed = true; current = j; goto 3; } }
goto 2;
Если индекс текущего элемента перестановки равен 0, то алгоритм завершает свою работу с отрицательным вердиктом.
if (current == 0) КОНЕЦ (асинхронная модель поведения является не корректной относительно данной асинхронной модели требований)
В противном случае алгоритм переинициализирует текущий счетчик числа точек ветвления и уменьшает индекс текущего элемента перестановки на единицу.
bound[current] = n-current; current--;
Если индекс текущего элемента перестановки оказался меньше индекса наибольшего элемента пути, содержащего актуальное множество состояний модели требований, то значение последнего устанавливается равным значению первого.
if (current < processed) processed = current;
Алгоритм переходит к шагу 9.
goto 9;
Доказательство корректности данного алгоритма представлено в [].
Частичный порядок

Обратим внимание на тот факт, что оценка сложности алгоритма O(n!) получена для класса детерминированных моделей поведения, для недетерминированных моделей сложность становится еще больше. Но даже при использовании детерминированных моделей требования применимость алгоритма сильно ограничена: при числе взаимодействий, превышающем несколько десятков время работы становится неприемлемо большим. Поэтому при применении рассматриваемого метода необходимо учитывать имеющиеся ограничения на размерность модели поведения, участвующей в задаче оценки корректности.
Архитектура UniTesK для систем с синхронным интерфейсом
Настоящая глава состоит из четырех разделов. Первые три раздела посвящены рассмотрению математических моделей и принципов решения основных задач тестирования:
задачи оценки корректности поведения тестируемой системы; задачи генерации тестовых данных; задачи оценки качества тестирования.
Четвертый раздел посвящен обсуждению унифицированной архитектуры теста, определяющей архитектуру всех тестовых систем, построенных по технологии UniTesK для систем с синхронным интерфейсом.
Математические модели, описанные в данной главе, несколько отличаются от традиционных описаний технологии UniTesK [, , ], что обусловлено попыткой взглянуть на технологию UniTesK с точки зрения ее практического использования.
Асинхронные функции
Для вычисления функций в распределенных взаимодействующих автоматах реализуется посредством использования выделенных взаимодействующих автоматов, получающих входные параметры функции и возвращающих результат.
Асинхронной функцией AF из множества входных значений IS во множество выходных значений OS называется взаимодействующий автомат SA = ( S, s0, X, Y, E, Q ), в котором
PY = { callAF,is | is


























e1 = ( s1, py1, s'1 )










Данные ограничения определяют ту специфическую роль, которую играют сообщения из PY и RX в работе автомата SA. Эта роль заключается в том, что функционирование автомата SA состоит из последовательных циклов, каждый из которых начинается получением параметризующей реакции callAF,ip и завершается посылкой результирующего стимула resultAF,op. Внутри этого цикла автомат SA произвольным образом взаимодействует со своим окружением, но только посредством сообщений, не входящих в PY

Множество всех асинхронных функций, у которых множество входных значений равно IS, а множество выходных значений равно OS, мы будем обозначать как Ã(IS,OS).
Чтобы работа распределенного взаимодействующего автомата завершилась, необходимо, чтобы все составляющие его автоматы перешли в заключительное состояние. Для этого вместо асинхронных функций обычно используют их замыкания по выделенному множеству терминирующих реакций.
Замыканием взаимодействующего автомата ( S, s0, X, Y, E, Q ) по множеству реакций R мы будем называть взаимодействующий автомат ( S', s'0, X', Y', E', Q' ), в котором
S' = S








Замыкание взаимодействующего автомата дополняет исходный автомат специальным завершающим состоянием и множеством переходов, ведущих в это состояние изо всех остальных состояний по получению реакции из множества R.
Асинхронные сценарные функции
Для описания стимулов графа автоматного сценария в асинхронном случае так же, как и в синхронном, используется понятие сценарной функции. В данном случае, в качестве сценарной функции выступает обычная асинхронная функция, а множество допустимых стимулов определяется на основе множества ее входных параметров.
Асинхронной сценарной функцией мы будем называть асинхронную функцию, в которой множество входных значений может быть произвольным, а множество выходных значений Bool состоит из двух элементов true и false.
Множество всех асинхронных сценарных функций, у которых множество входных значений равно IS, мы будем обозначать как Σ(IS).
Асинхронным автоматным тестовым сценарием со сценарными функциями для целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется семерка ( DA, Afsm, VG, XG, vg0, α,

DA - асинхронный тестовый сценарий для целевой системы с асинхронным интерфейсом ( X, Y, Z ), Afsm ( Sfsm, s0, Xfsm, Yfsm, Efsm, Qfsm ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый ведущим автоматом асинхронного тестового сценария DA, VG - множество состояний графа сценария, XG - множество стимулов графа сценария, vg0 - начальное состояние графа сценария, α - неизбыточный алгоритм движения по графу сценария,


и для которой выполнены следующие ограничения:
замыкания взаимодействующих автоматов Σi по множеству { stop, abort } входят в состав DA, причем все эти вхождения и вхождение Afsm в DA различаются между собой,







где XGi = { xg








множества состояний графа сценария VG, множества стимулов графа сценария XG, функции π: π(vg) = { xg




является асинхронным автоматным тестовым сценарием для целевой системы с асинхронным интерфейсом ( X, Y, Z ).
Асинхронные тесты
Асинхронным тестом целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется конечное или бесконечное частично упорядоченное мультимножество асинхронных взаимодействий ( P,

Асинхронный тест ( P,



Определение 15.
Асинхронным тестовым сценарием для целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется распределенный взаимодействующий автомат DA, в котором
множество стимулов совпадает с X; множество реакций совпадает с Y







Состояния взаимодействующих автоматов, из которых выходят только принимающие переходы, помеченные сообщениями из Y, будут далее называться промежуточными.
Асинхронный тестовый сценарий предназначен для управлением процессом тестирования систем с асинхронным интерфейсом. Такой тестовый сценарий подает тестовые стимулы целевой системе и получает от нее непосредственные и отложенные реакции, используя эту информацию для продолжения тестирования.
Множество всех асинхронных тестовых сценариев для целевой системы с асинхронным интерфейсом ( X, Y, Z ) будем обозначать символом

Асинхронный тест ( P,



Асинхронный тестовый сценарий определяет правила посылки тестовых стимулов, которые могут зависеть от ответа целевой системы. Результатом работы сценария является асинхронный тест, состоящий из набора взаимодействий с целевой системой и информации о порядке, в котором происходили эти взаимодействия. Этот порядок в точности соответствует порядку взаимодействий между тестовым сценарием и целевой системой, наблюдаемому в процессе работы тестового сценария.
При наличии некоторой среды между тестовой системой и целевой системой, например, сетевого соединения, которое не гарантирует сохранения порядка сообщений, предполагается, что эта среда включается в тестовый сценарий и моделируется в нем явно. В качестве альтернативы включения среды между тестовой системой и целевой системой в состав тестового сценария можно использовать включение этой среды в состав целевой системы, но в этом случае все требования к поведению целевой системы необходимо формулировать с учетом поведения этой среды.
Определение 16.
Механизмом построения асинхронного тестового сценария будем называть функцию, значением которой является асинхронный тестовый сценарий.
Также как и для обычных тестовых сценариев, для асинхронных тестовых сценариев мы определим автоматный механизм их построения, который обеспечивает автоматическое формирование последовательности тестовых воздействий на основе обхода ориентированного графа.
Асинхронный тестовый сценарий dfsm
Основным механизмом построения тестовых сценариев в синхронном случае является механизм построения тестового сценария dfsm. Этот механизм основан на неизбыточном алгоритме обхода на классе детерминированных сильно-связных конечных ориентированных графов αdfsm[]. Для стационарного тестирования асинхронных систем данный алгоритм обхода также будет выступать в качестве одного из основных.
Определение 19.
Асинхронным тестовым сценарием dfsm относительно асинхронной модели требований A ( V, X, Y, Z, E ) с множеством стабильных состояний VS


Любое конечное функционирование алгоритма обхода αdfsm приводит
либо к обнаружению нарушения требований детерминированности или сильно-связности графа сценария, либо к построению обхода этого графа.
Таким образом, если граф сценария при любом корректном функционировании целевой системы является детерминированным и сильно-связным, то в результате успешной работы асинхронного тестового сценария dfsm путь, пройденный по графу сценария, является обходом этого графа. В этом случае, в каждом достижимом состоянии графа сценария будет вызвана каждая допустимая в данном состоянии асинхронная сценарная функция. Это позволяет строить асинхронные тестовые сценарии на основе так называемой автоматной композиции, которая продемонстрировала свои достоинства в ходе применения технологии UniTesK для тестирования синхронных систем различного рода.
Однако, при тестировании асинхронных систем недетерминированное поведение встречается значительно чаще, так как в случае параллельных взаимодействий результат может определяться последовательностью внутренних событий целевой системы, не поддающихся наблюдению и тем более управлению со стороны тестовой системы. Поэтому потребность в использовании алгоритмов обхода, способных работать с недетерминированными графами, для асинхронных тестовых сценариев выше, чем в синхронном случае. Один из таких алгоритмов, мы рассмотрим в следующем разделе.
Автоматный механизм построения асинхронного тестового сценария
Асинхронным автоматным тестовым сценарием для целевой системы с асинхронным интерфейсом ( X, Y, Z ) называется пятерка ( DA, Afsm, IG, vg0, α ), где
DA - асинхронный тестовый сценарий для целевой системы с асинхронным интерфейсом ( X, Y, Z ), Afsm = ( Sfsm, s0, Xfsm, Yfsm, Efsm, Qfsm ) - выделенный взаимодействующий автомат, входящий в состав DA, и называемый ведущим автоматом асинхронного тестового сценария DA, IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария, vg0

и для которой выполнены следующие ограничения:
Sfsm = ( VG x EG* x (XG


текущую вершину графа сценария vg, пройденный маршрут в графе сценария path (здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG), последний посланный стимул графа, на который не был получен ответ, либо ε, обозначающее отсутствие такового стимула;
s0 = ( vg0,


Xfsm = { startvg,xg | vg






{ ( ( vg, path, ε ), stop, final ) | α( IG, vg, path ) = τ }

{ ( ( vg, path, xg ), finishvg*, ( vg', path', ε ) |
vg' = vg*

path' = path ^ ( vg, xg, vg' )
}

{ ( ( vg, path, xg ), abort, final ) }
Qfsm = { final } - множество заключительных состояний ведущего автомата состоит из единственного состояния final.
Автоматным механизмом построения асинхронного тестового сценария называется функция, которая преобразует асинхронный автоматный тестовый сценарий ( DA, Afsm, IG, vg0, α ) в асинхронный тестовый сценарий DA.
Работа автоматного тестового сценария устроена следующим образом. Граф сценария описывает некоторым образом пространство тестовых ситуаций. Ведущий автомат двигается по данному графу, используя заданный алгоритм движения.
Алгоритм движения выбирает стимул графа, который необходимо подать в текущей вершине. Ведущий автомат посылает сообщение, соответствующее текущей вершине и выбранному стимулу. Это сообщение обрабатывается другими взаимодействующими автоматами, входящими в состав DA, и преобразуется в набор воздействий на целевую систему. По завершении обработки этого сообщения, ведущему автомату посылается либо новая вершина графа, либо уведомление об аварийном завершении работы. В первом случае, ведущий автомат повторяет рассмотренный цикл до тех пор, пока алгоритм движения не завершит свою работу. Во втором случае, работа тестового сценария завершается.
Автоматный механизм построения тестового сценария
Ориентированным графом будем называть тройку G = ( VG, XG, EG ), в которой:
VG - множество вершин графа; XG - множество стимулов графа; EG

Ориентированный граф G = ( VG, XG, EG )называется конечным, если множества VG, XG, и EG являются конечными.
Стимул s



Ориентированный граф G = ( VG, XG, EG ) называется детерминированным, если для каждой вершины u



Последовательность дуг ( e1, e2, …, en ) ориентированного графа G = ( VG, XG, EG ) называется маршрутом, если для каждого i = 1, …, n-1 конечная вершина перехода ei совпадает с начальной вершиной перехода ei+1. При этом мы будем говорить, что маршрут ведет из начальной вершины перехода e1 в конечную вершину перехода en.
Бесконечным маршрутом мы будем называть бесконечную последовательность переходов, любой префикс которой является конечным маршрутом.
Ориентированный граф G = ( VG, XG, EG ) называется сильно-связным, если для любых двух его вершин v и v' существует маршрут ( e1, e2, …, en ), ведущий из вершины v в вершину v'.
Обходом конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1
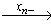


Определение 6.
Алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v



Ориентированным графом будем называть тройку G = ( VG, XG, EG ), в которой:
VG - множество вершин графа; XG - множество стимулов графа; EG

Ориентированный граф G = ( VG, XG, EG )называется конечным, если множества VG, XG, и EG являются конечными.
Стимул s



Ориентированный граф G = ( VG, XG, EG ) называется детерминированным, если для каждой вершины u



Последовательность дуг ( e1, e2, …, en ) ориентированного графа G = ( VG, XG, EG ) называется маршрутом, если для каждого i = 1, …, n-1 конечная вершина перехода ei совпадает с начальной вершиной перехода ei+1. При этом мы будем говорить, что маршрут ведет из начальной вершины перехода e1 в конечную вершину перехода en.
Бесконечным маршрутом мы будем называть бесконечную последовательность переходов, любой префикс которой является конечным маршрутом.
Ориентированный граф G = ( VG, XG, EG ) называется сильно-связным, если для любых двух его вершин v и v' существует маршрут ( e1, e2, …, en ), ведущий из вершины v в вершину v'.
Обходом конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1
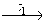
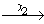
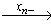


Определение 6.
Алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v



Функционированием алгоритма движения α на ориентированном графе G = ( VG, XG, EG ) с начальной вершины v0

начальная вершина v1 первой дуги маршрута e1 = ( v1, x1, v'1 ) совпадает с начальной вершиной v0; в каждой дуге маршрута ei = ( vi, xi, v'i ) стимул xi равен α( A, vi, ( e1, …, ei-1 ) ) - значению алгоритма движения α на автомате A, начальной вершине vi и пройденном маршруте ( e1, …, ei-1 ); если дуга ei = ( vi, xi, v'i ) является последней в последовательности, то α( A, v'i, ( e1, …, ei ) ) = τ.
Алгоритм движения α называется алгоритмом обхода на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом графа G.
Алгоритм движения α называется неизбыточным, если для любых двух конечных ориентированных графов G1 = ( VG1, XG1, EG1 ) и G2 = ( VG2, XG2, EG2 ), для любой вершины v

Преимущество неизбыточных алгоритмов заключается в том, что для начала их работы не требуется полное описание ориентированного графа. Вся информация о вершинах и дугах графа, используемая неизбыточным алгоритмом, может быть извлечена в процессе движения по графу.
В работах [, , ] представлено исследование неизбыточных алгоритмов обхода различных классов графов. В частности, в [] рассмотрен неизбыточный алгоритм обхода αdfsm на классе детерминированных сильно-связных конечных ориентированных графах.
Этот алгоритм используется в технологии UniTesK в качестве основного алгоритма для построения последовательностей тестовых воздействий.
Неизбыточным описанием ориентированного графа называется тройка ( VG, XG, π ), где
VG - множество вершин графа, XG - множество стимулов графа, π : VG


Неизбыточное описание ориентированного графа содержит все необходимое для работы неизбыточного алгоритма движения. С другой стороны, для разработчика теста значительно проще создать такое описание, чем описывать граф в явном виде. Поэтому в технологии UniTesK неизбыточное описание графа нашло свое применение при определении тестовых сценариев.
Автоматным тестовым сценарием для целевой системы с интерфейсом ( X, Y, V ) называется семерка ( IG, vg0, α, S, ρ, γ, η ), где
IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария, vg0 : V





Автоматным механизмом построения тестового сценария называется функция, преобразующая автоматный тестовый сценарий ( IG, vg0, α, S, ρ, γ, η ) в тестовый сценарий, посредством вспомогательного определения тестового сценария с внутренними переходами σε = ( ( S', A, B, E, Q ), s0 ) по следующим правилам:
S' = VG x S

текущей вершины графа сценария vg, текущего состояния сценария s, которое может принимать дополнительное значение ε, которое означает неинициализированное состояние, текущего состояния целевой системы v, пройденного маршрута в графе сценария path. Здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG.
множество стимулов A = X


















)
}, где использовались следующие сокращения xg ≡ α( IG, vg, path ); state( a, b, v ) = a, если a













- инициализирующая функция, которая устанавливает следующие начальные значения: текущая вершина графа сценария определяется при помощи функции инициализации графа сценария; текущее состояние сценария s принимает значение, вычисленное посредством инициализирующей функции первого сценарного воздействия, если таковое найдено при помощи алгоритм движения α, неинициализированное значение, в противном случае; текущее состояние целевой системы инициализируется параметром функции, пройденный маршрут инициализируется пустым списком.
Далее для построения тестового сценария автоматный механизм использует определенное ранее преобразование тестового сценария с внутренними переходами в тестовый сценарий без внутренних переходов.
Работа автоматного механизма построения тестового сценария устроена следующим образом. Граф сценария описывает некоторым образом пространство тестовых ситуаций. Автоматный механизм двигается по данному графу, используя заданный алгоритм движения.
Алгоритм движения выбирает стимул, который необходимо подать в текущей вершине. Автоматный механизм определяет тестовый сценарий, который приписан паре вершина-стимул графа сценария, и выполняет его. По результатам выполнения механизм вычисляет новую вершину графа сценария и повторяет этот цикл до тех пор, пока алгоритм движения не завершит свою работу.
Все тестовые сценарии, приписанные к графу сценария, разделяют общее состояние, которое позволяет им накапливать информацию о процессе тестирования. После завершения каждого сценария автоматный механизм обновляет это состояние при помощи функции рестарта сценария. Благодаря этому, один и тот же тестовый сценарий может успешно применяться несколько раз подряд.
Пара отображений γ и η определяет дуги графа сценария, основываясь на поведении целевой системы. Таким образом, граф сценария строится динамически посредством применения этих отображений. В него входят те дуги, которые были "пройдены" в процессе тестирования.
Функционированием алгоритма движения α на ориентированном графе G = ( VG, XG, EG ) с начальной вершины v0

начальная вершина v1 первой дуги маршрута e1 = ( v1, x1, v'1 ) совпадает с начальной вершиной v0; в каждой дуге маршрута ei = ( vi, xi, v'i ) стимул xi равен α( A, vi, ( e1, …, ei-1 ) ) - значению алгоритма движения α на автомате A, начальной вершине vi и пройденном маршруте ( e1, …, ei-1 ); если дуга ei = ( vi, xi, v'i ) является последней в последовательности, то α( A, v'i, ( e1, …, ei ) ) = τ.
Алгоритм движения α называется алгоритмом обхода на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом графа G.
Алгоритм движения α называется неизбыточным, если для любых двух конечных ориентированных графов G1 = ( VG1, XG1, EG1 ) и G2 = ( VG2, XG2, EG2 ), для любой вершины v

Преимущество неизбыточных алгоритмов заключается в том, что для начала их работы не требуется полное описание ориентированного графа. Вся информация о вершинах и дугах графа, используемая неизбыточным алгоритмом, может быть извлечена в процессе движения по графу.
В работах [, , ] представлено исследование неизбыточных алгоритмов обхода различных классов графов. В частности, в [] рассмотрен неизбыточный алгоритм обхода αdfsm на классе детерминированных сильно-связных конечных ориентированных графах.
Этот алгоритм используется в технологии UniTesK в качестве основного алгоритма для построения последовательностей тестовых воздействий.
Неизбыточным описанием ориентированного графа называется тройка ( VG, XG, π ), где
VG - множество вершин графа, XG - множество стимулов графа, π : VG


Неизбыточное описание ориентированного графа содержит все необходимое для работы неизбыточного алгоритма движения. С другой стороны, для разработчика теста значительно проще создать такое описание, чем описывать граф в явном виде. Поэтому в технологии UniTesK неизбыточное описание графа нашло свое применение при определении тестовых сценариев.
Автоматным тестовым сценарием для целевой системы с интерфейсом ( X, Y, V ) называется семерка ( IG, vg0, α, S, ρ, γ, η ), где
IG = ( VG, XG, π ) - неизбыточное описание ориентированного графа, называемого графом сценария, vg0 : V





Автоматным механизмом построения тестового сценария называется функция, преобразующая автоматный тестовый сценарий ( IG, vg0, α, S, ρ, γ, η ) в тестовый сценарий, посредством вспомогательного определения тестового сценария с внутренними переходами σε = ( ( S', A, B, E, Q ), s0 ) по следующим правилам:
S' = VG x S

текущей вершины графа сценария vg, текущего состояния сценария s, которое может принимать дополнительное значение ε, которое означает неинициализированное состояние, текущего состояния целевой системы v, пройденного маршрута в графе сценария path. Здесь множество EG* обозначает множество всех конечных списков элементов из множества дуг EG = VG x XG x VG.
множество стимулов A = X


















)
}, где использовались следующие сокращения xg ≡ α( IG, vg, path ); state( a, b, v ) = a, если a













- инициализирующая функция, которая устанавливает следующие начальные значения: текущая вершина графа сценария определяется при помощи функции инициализации графа сценария; текущее состояние сценария s принимает значение, вычисленное посредством инициализирующей функции первого сценарного воздействия, если таковое найдено при помощи алгоритм движения α, неинициализированное значение, в противном случае; текущее состояние целевой системы инициализируется параметром функции, пройденный маршрут инициализируется пустым списком.
Далее для построения тестового сценария автоматный механизм использует определенное ранее преобразование тестового сценария с внутренними переходами в тестовый сценарий без внутренних переходов.
Работа автоматного механизма построения тестового сценария устроена следующим образом. Граф сценария описывает некоторым образом пространство тестовых ситуаций. Автоматный механизм двигается по данному графу, используя заданный алгоритм движения.
Алгоритм движения выбирает стимул, который необходимо подать в текущей вершине. Автоматный механизм определяет тестовый сценарий, который приписан паре вершина-стимул графа сценария, и выполняет его. По результатам выполнения механизм вычисляет новую вершину графа сценария и повторяет этот цикл до тех пор, пока алгоритм движения не завершит свою работу.
Все тестовые сценарии, приписанные к графу сценария, разделяют общее состояние, которое позволяет им накапливать информацию о процессе тестирования. После завершения каждого сценария автоматный механизм обновляет это состояние при помощи функции рестарта сценария. Благодаря этому, один и тот же тестовый сценарий может успешно применяться несколько раз подряд.
Пара отображений γ и η определяет дуги графа сценария, основываясь на поведении целевой системы. Таким образом, граф сценария строится динамически посредством применения этих отображений. В него входят те дуги, которые были "пройдены" в процессе тестирования.
Формализация задачи
Проблема оценки корректности поведения целевой системы является одной из основных задач функционального тестирования. В технологии UniTesK эта задача решается следующим образом.
Поведение целевой системы в процессе тестирования представляется формальным образом в виде модели поведения, которая состоит из набора взаимодействий целевой системы со своим окружением. Требования, предъявляемые к функциональности целевой системы, описываются формально в виде модели требований. На декартовом произведении всех возможных моделей поведения и всех возможных моделей требований определяется формальное отношение "удовлетворяет", которое соответствует неформальному пониманию отношения "удовлетворяет" между поведением целевой системы и функциональными требованиями. В результате, на уровне математической модели, задача оценки корректности поведения целевой системы эквивалентна проверке наличия отношения "удовлетворяет" между моделью поведения целевой системы и моделью требований. Рассмотренный подход проиллюстрирован на рисунке 2.
Рассмотрим формальные определения моделей поведения и требований.
Формальные методы и тестирование программного обеспечения
В последнее время наблюдается бурное развитие компьютерных технологий. Они проникают во все сферы деятельности человека и оказывают все большее влияние на его жизнь. Системы управления транспортом и автоматизированные линии производства, банковские платежные системы и телекоммуникационные сети, медицинские системы обеспечения жизнедеятельности и интеллектуальные дома - все это является неотъемлемой частью современного мира.
Однако, чем большее значение отводится компьютерным системам, тем выше становится цена их ошибок. Как показывает практика, наиболее уязвимым местом компьютерных систем с этой точки зрения является программное обеспечение. Так, ошибка в одном программном модуле многомиллионного межпланетного корабля Mars Climate Orbiter привела к его гибели в атмосфере Марса после более чем девятимесячного полета [, ].
Более того, некорректное поведение современных программных систем влечет не только огромные убытки, но и приводит к гибели людей. Например, ошибки в программном обеспечении медицинского оборудования Therac-25 привели к получению повышенной дозы радиации и последующей смерти 7 пациентов [, ]. А арифметическая ошибка в программном обеспечении комплекса противовоздушной обороны Patriot не позволила вовремя обнаружить иракскую ракету, что привело к гибели 28 солдат во время ирако-американской войны 1991 года []. И это только малая часть уже имевших место прецедентов.
С нарастанием сложности и важности задач, решаемых программными системами, проблема обеспечения их качества становится все острее. Много надежд на существенный прогресс в этом направлении связывается с развитием формальных методов.
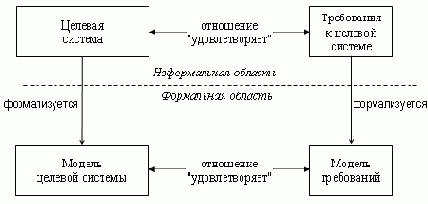
Рисунок 1.Схема работы методов аналитической верификации и проверки моделей
В широком смысле, под формальными методами понимаются любые попытки использования математических подходов к разработке программного обеспечения с целью повышения его качества[]. Как правило, для этого используются математические модели различных сущностей, участвующих в процессе разработки.
В последнее время наблюдается бурное развитие компьютерных технологий. Они проникают во все сферы деятельности человека и оказывают все большее влияние на его жизнь. Системы управления транспортом и автоматизированные линии производства, банковские платежные системы и телекоммуникационные сети, медицинские системы обеспечения жизнедеятельности и интеллектуальные дома - все это является неотъемлемой частью современного мира.
Однако, чем большее значение отводится компьютерным системам, тем выше становится цена их ошибок. Как показывает практика, наиболее уязвимым местом компьютерных систем с этой точки зрения является программное обеспечение. Так, ошибка в одном программном модуле многомиллионного межпланетного корабля Mars Climate Orbiter привела к его гибели в атмосфере Марса после более чем девятимесячного полета [, ].
Более того, некорректное поведение современных программных систем влечет не только огромные убытки, но и приводит к гибели людей. Например, ошибки в программном обеспечении медицинского оборудования Therac-25 привели к получению повышенной дозы радиации и последующей смерти 7 пациентов [, ]. А арифметическая ошибка в программном обеспечении комплекса противовоздушной обороны Patriot не позволила вовремя обнаружить иракскую ракету, что привело к гибели 28 солдат во время ирако-американской войны 1991 года []. И это только малая часть уже имевших место прецедентов.
С нарастанием сложности и важности задач, решаемых программными системами, проблема обеспечения их качества становится все острее. Много надежд на существенный прогресс в этом направлении связывается с развитием формальных методов.

Рисунок 1.Схема работы методов аналитической верификации и проверки моделей
В широком смысле, под формальными методами понимаются любые попытки использования математических подходов к разработке программного обеспечения с целью повышения его качества[]. Как правило, для этого используются математические модели различных сущностей, участвующих в процессе разработки.
Примерами таких моделей могут служить модель исходных требований к разрабатываемой системе, модель архитектуры системы или модель реализации системы.
Одним из основных направлений в области формальных методов являются методы доказательства корректности программ, такие как методы аналитической верификации и проверки моделей [, , , ]. В этих методах доказательство корректности программ строится по следующей схеме. Для данной программной системы создаются математическая модель требований к системе и математическая модель реализации этой системы. После чего доказывается наличие отношения "удовлетворяет" между этими двумя моделями, что и рассматривается как доказательство корректности программы (рисунок 1). Существует также целый набор вариаций подхода. Например, в качестве модели требований может выступать модель программной системы более высокого уровня абстракции, или доказательство корректности может сводиться к доказательству непротиворечивости одной из математических моделей.
Однако, несмотря на большие усилия, вложенные в развитие данного направления, на настоящий момент так и не появилось методов доказательства корректности программ, которые смогли бы предоставить приемлемые решения для обеспечения качества реальных программных систем. В результате, одним из основных средств обеспечения качества программных систем было и остается тестирование: при разработке программ с повышенными требованиями к надежности доля затрат на тестирование в бюджете проекта может достигать 80%.
Многочисленные исследования в области формальных методов нашли свое отражение и в развитии новых технологий тестирования. Одно из наиболее активно развивающихся направлений - тестирование на основе моделей, уже успело показать свои преимущества в целом ряде крупных индустриальных проектов [, , , , , , ].
Тестирование на основе моделей позволяет систематизировать и автоматизировать процесс разработки тестовых наборов посредством использования различного рода математических моделей.И в тех случаях, когда небольшого ручного тестирования оказывается недостаточно для обеспечения требуемого уровня качества программного обеспечения, тестирование на основе моделей позволяет добиться существенного повышения качества тестирования с затратами меньшими, чем при использовании других подходов.

Рисунок 2. Схема работы технологии UniTesK относительно формальных методов
Примерами таких моделей могут служить модель исходных требований к разрабатываемой системе, модель архитектуры системы или модель реализации системы.
Одним из основных направлений в области формальных методов являются методы доказательства корректности программ, такие как методы аналитической верификации и проверки моделей [, , , ]. В этих методах доказательство корректности программ строится по следующей схеме. Для данной программной системы создаются математическая модель требований к системе и математическая модель реализации этой системы. После чего доказывается наличие отношения "удовлетворяет" между этими двумя моделями, что и рассматривается как доказательство корректности программы (рисунок 1). Существует также целый набор вариаций подхода. Например, в качестве модели требований может выступать модель программной системы более высокого уровня абстракции, или доказательство корректности может сводиться к доказательству непротиворечивости одной из математических моделей.
Однако, несмотря на большие усилия, вложенные в развитие данного направления, на настоящий момент так и не появилось методов доказательства корректности программ, которые смогли бы предоставить приемлемые решения для обеспечения качества реальных программных систем. В результате, одним из основных средств обеспечения качества программных систем было и остается тестирование: при разработке программ с повышенными требованиями к надежности доля затрат на тестирование в бюджете проекта может достигать 80%.
Многочисленные исследования в области формальных методов нашли свое отражение и в развитии новых технологий тестирования. Одно из наиболее активно развивающихся направлений - тестирование на основе моделей, уже успело показать свои преимущества в целом ряде крупных индустриальных проектов [, , , , , , ].
Тестирование на основе моделей позволяет систематизировать и автоматизировать процесс разработки тестовых наборов посредством использования различного рода математических моделей.И в тех случаях, когда небольшого ручного тестирования оказывается недостаточно для обеспечения требуемого уровня качества программного обеспечения, тестирование на основе моделей позволяет добиться существенного повышения качества тестирования с затратами меньшими, чем при использовании других подходов.

Рисунок 2. Схема работы технологии UniTesK относительно формальных методов
Работа по тестированию MSR IPv6 получила продолжение в проекте по тестированию функций Mobile IPv6 на примере реализации Microsoft MIPv6 для Windows CE 4.1 и Windows XP. В этом проекте было проведено тестирование соответствия реализации базовых функций IPv6 в Windows CE на основе спецификаций и тестов, разработанных для MSR IPv6. Кроме того, проводилось тестирование на соответствие реализации ряда функций протокола Mobile IPv6 спецификациям протокола, а также соответствие реализации служебного протокола MLD (Multicast Listener Discovery) спецификации протокола.
Требования к реализации Mobile IPv6 извлекались из 13-го проекта стандарта Mobile IPv6, так как именно эту спецификацию поддерживала тестируемая реализация. Требования к реализации MLD извлекались из спецификаций первой версии протокола MLD, RFC 2710. В качестве дополнительных источников требований использовались RFC 2462 и RFC 2473. Эти требования были описаны в виде асинхронной модели требований, которая в дальнейшем использовалась для оценки корректности поведения тестируемой системы.
Для организации тестирования использовалась распределенная архитектура тестового набора, в рамках которой в процессе тестирования участвовало несколько систем, объединенных локальной сетью. На выделенной инструментальной машине решались основные задачи тестовой системы, заключающиеся в организации тестовых воздействий и оценке корректности поведения тестируемой системы. Другие машины использовались для оказания тестовых воздействий на тестируемую систему и получения реакций от нее.
Генерация тестовых данных
В этом разделе мы остановимся на проблеме генерации тестовых данных. Предположим, что мы автоматизировали процесс оценки корректности поведения целевой системы, и для каждого взаимодействия с тестируемой системой можем автоматически вынести вердикт. Но как организовать эти взаимодействия?
Описывать их вручную - очень утомительно и накладно. Автоматически генерировать последовательности тестовых воздействий - возможно, но качество, как правило, оказывается весьма невысоким. Технология UniTesK предлагает следующее компромиссное решение.
UniTesK разбивает задачу генерации тестовых воздействий на две подзадачи: генерацию семантически значимых значений отдельных типов данных, являющихся параметрами тестовых воздействий, и организацию сложных последовательностей взаимодействий, достигающих необходимый уровень покрытия.
Первая подзадача не может быть решена автоматически, так как в общем случае сводится к решению системы уравнений произвольной сложности. С другой стороны, для разработчика теста, как правило, не является большой проблемой указать множество семантически значимых значений определенного типа. Поэтому технология UniTesK перекладывает ответственность за решение этой задачи на разработчика, предоставляя ему существенную помощь в решении второй подзадачи.
Для организации сложных последовательностей тестовых воздействий на целевую систему в технологии UniTesK разработан специальный механизм построения тестового сценария. Этот механизм обеспечивает систематизированный обход заданного пространства тестовых ситуаций, посредством осуществления тестовых воздействий. При этом от разработчика тестов требуется только задание состояния сценария, согласованного с набором тестовых воздействий.
В основе механизма построения тестового сценария лежит граф. Состояния этого графа отражают различные "интересные" тестовые ситуации, а его дуги соответствуют заданным последовательностям тестовых воздействий. Тестовая система строит обход графа, осуществляя тестовые воздействия, приписанные к его дугам и, таким образом, решает задачу организации сложных последовательностей взаимодействий. Одним из вариантов построения графа является обобщение абстрактного автомата, описывающего требования, на основании наблюдения за поведением тестируемой системы. В этом случае граф тестового сценария является высокоуровневой моделью целевой системы, извлекаемой из наблюдения за ее поведением в процессе тестирования.
Формальные определения модели построения тестового сценария будут рассмотрены в последующих разделах.
Генерация тестовых данных для асинхронных систем
В данном разделе мы рассмотрим проблему генерации тестовых данных для асинхронных систем. Решение этой проблемы сильно осложняется большой временной сложностью алгоритмов оценки корректности поведения асинхронных систем. Область применимости этих алгоритмов ограничена асинхронными моделями поведения, состоящими из нескольких десятков взаимодействий.
Одного теста такого размера явно не достаточно для достижения приемлемого качества тестирования. Построение наборов независимых тестов небольшого размера приведет к потере одного из основных достоинств технологии UniTesK - автоматическому построению сложных последовательностей тестовых воздействий.
Компромиссное решение, позволяющее совместить генерацию тестовых последовательностей с ограничениями на размеры модели поведения, подвергающейся оценки корректности, было предложено в работе []. Идея этого подхода заключается в использовании автоматных тестовых сценариев для построения обхода графа, в котором каждой дуге приписан асинхронный тест небольшого размера. Для реализации такого подхода требуется, чтобы целевая система после получения любого набора асинхронных воздействий за конечное время переходила в состояние, в котором она не должна выдавать ни одной асинхронной реакции до получения следующего воздействия.
С учетом этого ограничения данный подход позволяет сохранить автоматическое построение сложных последовательностей тестовых воздействий, несмотря на ограниченную применимость алгоритма оценки корректности поведения.
В последующих разделах мы рассмотрим вопрос построения тестов для систем с асинхронным интерфейсом более формально.
Граф автоматного тестового сценария
Неизбыточное описание графа сценария не является описанием единственного графа. Оно только определяет набор элементов, из которых можно построить граф. Фактический граф определяется в процессе функционирования автоматного тестового сценария.
Предположим, что σaut = ( IG, vg0, α, S, ρ, γ, η ) - автоматный тестовый сценарий для целевой системы с интерфейсом ( X, Y, V ). Предположим, что σ = ( С, s0 ) - тестовый сценарий, полученный посредством применения автоматного механизма построения тестового сценария к σaut. Тогда функционированиями автоматного тестового сценария σaut на целевой системе с начальным состоянием v0

Заметим, что согласно определению автоматного механизма построения тестового сценария состояниями управляющего автомата sj являются четверки ( vgj, sj, vj, pathj )


Графом автоматного тестового сценария σaut = ( IG = ( VG, XG, π ), vg0, α, S, ρ, γ, η ) при функционировании σaut { ej = ( sj, aj, bj, s'j ) } называется ориентированный граф G' = ( VG', XG', EG' ), в котором:
множество вершин VG' = VG; множество стимулов XG' = XG; множество дуг EG' = { eg


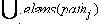
Лемма.
Граф автоматного тестового сценария ( IG, vg0, α, S, ρ, γ, η ) при любом функционировании { ej = ( sj, aj, bj, s'j ) } удовлетворяет неизбыточному описанию IG.
Действительно. Граф состоит из дуг пути в графе, пройденного неизбыточным алгоритмом движения по графу, который выбирает стимулы только из множества, допустимых в текущем состоянии.
Инструментальная поддержка тестирования систем с асинхронными интерфейсами
В настоящей главе мы рассмотрим инструментальную поддержку описываемого подхода к тестированию систем с асинхронным интерфейсом. Данная поддержка реализована в виде расширения набора инструментов CTesK, поддерживающих процесс тестирования по технологии UniTesK на платформе языка C.
Ядро операционной системы реального времени
Наиболее значимой работой по тестированию асинхронных аспектов поведения многопотоковых и многопроцессных систем является проект по тестированию ядра POSIX-совместимой операционной системы реального времени ОС2000. Эта операционная система предоставляет пользователю прикладной программный интерфейс, состоящий из 482 функций. В рамках проекта все функции были проанализированы и сгруппированы по подсистемам согласно реализуемой ими функциональности. Список подсистем приведен в таблице 2. Во втором столбце таблицы указано число интерфейсных функций, принадлежащих соответствующей подсистеме.
| Потоки управления | 39 | A1 |
| Планировщик | 10 | A1 |
| Сигналы | 19 | A1 |
| Синхронизация | 30 | A2 |
| Очереди сообщений | 10 | A2 |
| Прерывания | 14 | A1 |
| Время и таймеры | 25 | A1 |
| Поддержка многопроцессорности | 15 | A3 |
| Память | 9 | A3 |
| Ввод-вывод | 61 | A2 |
| Асинхронный ввод-вывод | 8 | A1 |
| Файловая система | 11 | A3 |
| Терминалы | 10 | A1 |
| Сокеты | 39 | A2 |
| IEEE 754 | 16 | A1 |
| Математические функции | 37 | S |
| Строковые функции | 50 | S |
| Функции протоколирования | 53 | A1 |
| Вспомогательные функции | 26 | S |
Таблица 2. Разбиение функций ОС2000 на подсистемы.
Анализ функциональности выделенных подсистем показал, что только три подсистемы из девятнадцати не требуют применения методов тестирования систем с асинхронным интерфейсом и могут быть полностью протестированы на основе методов синхронного тестирования. Эти подсистемы помечены в таблице 2 символом S. Они реализуют математические функции, функции для работы со строками и вспомогательные функции.
Остальные шестнадцать подсистем либо содержат в своем интерфейсе взаимодействия, инициируемые тестируемой системой, либо их тестирование не может быть проведено на требуемом уровне качества с использованием только последовательных взаимодействий. К первой группе относятся девять подсистем, помеченных символом A1, а ко второй группе - семь подсистем, помеченных символами A2 и A3.
Подсистема управления потоками содержит такие асинхронные реакции как:
старт нового потока управления; вызов функции инициализации во время динамической инициализации переменных; вызов функций свертывания и функций деструкторов локальных данных потока в процессе завершения работы потока.
В ходе проекта было выделено три класса функций прикладного программного интерфейса, для тестирования которых требуется применение асинхронных методов.
Первый класс функций составляют функции, приводящие к появлению явных асинхронных реакций, таких как сигналы, вызов функций обратного интерфейса, старт, приостановка и завершение потоков управления и т.д. Второй класс образуют блокируемые функции, управление из которых возвращается только при наступлении определенных условий, таких как освобождение требуемых ресурсов, поступление необходимого числа данных и т.д. В третий класс входят функции, которые должны обеспечивать корректность своей работы при одновременном вызове из различных потоков управления и для тестирования которых требуется одновременное участие целевой системы в нескольких взаимодействиях.
Одним из результатов проекта является подтверждение того, что во всех трех случаях использование предложенного метода тестирования систем с асинхронным интерфейсом позволяет преодолеть ограничения синхронного тестирования и обеспечить необходимый уровень качества тестирования. С другой стороны, проект продемонстрировал, что реализация метода тестирования асинхронных систем в системе тестирования CTesK предоставляет возможность тестирования действительно сложных целевых систем с нетривиальной функциональностью, таких как ядро операционной системы реального времени.
Компоненты распределенной операционной системы для сенсорных сетей
В дополнение к опыту тестирования телекоммуникационных систем предложенный подход применялся для тестирования асинхронных аспектов поведения многопроцессных и многопотоковых систем. Первым таким опытом был пилотный проект по тестированию отдельных компонентов TinyOS - распределенной операционной системы для сенсорных сетей, проведенной ИСП РАН совместно с российской компанией Luxoft.
Особенностью работы с TinyOS является то, что для написания компонентов используется специфический C-подобный язык nesC. На этом языке интерфейс компонентов операционной системы описывается двусторонним образом. С одной стороны описывается набор интерфейсных функций, предоставляемых данным компонентом, с другой стороны описывается набор функций, которые должен предоставить компонент, использующий сервисы данного компонента. Таким образом, функциональность каждой интерфейсной функции может заключаться не только в вычислении результата, но и в обращении с определенными значениями параметров к функциям пользователя, причем дальнейшее поведение может зависеть от результатов, полученных от этих пользовательских функций.
При описании требований к такого рода системам, вызов интерфейсной функции тестируемого компонента рассматривался в качестве стимула на целевую систему, а вызов пользовательской функции из тестируемого компонента - в качестве реакции целевой системы. Соответственно, данные, возвращаемые в тестируемый компонент из пользовательской функции, рассматривались в качестве стимула на целевую систему, а данные, возвращаемые из интерфейсной функции, - в качестве ее реакции.
Стимулы, моделирующие возврат управления из пользовательской функции, являлись достаточно специфичными, так как они могли быть посланы целевой системе только в ответ на специальный класс реакций, полученных с ее стороны. Тем не менее, работа с этими стимулами не вызвала никаких проблем. Ограничения на ситуации, когда можно подавать такие стимулы, были описаны в предусловии соответствующих спецификационных функций и автоматически отслеживались в процессе тестирования. Также эти ограничения учитывались при разработке тестовых сценариев, чтобы обеспечивать согласованность выполняемых тестовых воздействий с предусловиями стимулов.
В рамках проекта тестировался интерфейс TinyDB, предоставляющий доступ к показаниям распределенных сенсоров в виде операций чтения/записи виртуальной базы данных. Для него были формализованы требования к 6 интерфейсным операциям и разработаны 5 асинхронных тестовых сценариев. Результатом использования метода тестирования систем с асинхронным интерфейсом в данном проекте стала первая демонстрация возможности успешной работы этого метода за рамками телекоммуникационных протоколов.
Основным разработчиком спецификаций и тестовых сценариев во всех четырех проектах, рассмотренных выше, является Николай Пакулин.
Литература
| 1. | Euler E.E., Jolly S.D., Curtis H.H. The Failures of the Mars Climate Orbiter and Mars Polar Lander: A Perspective from the People Involved // Proceedings of Guidance and Control 2001. American Astronautical Society, AAS 01-074, 2001. |
| 2. | Report on the Loss of the Mars Climate Orbiter Mission. JPL D-18441, 1999. |
| 3. | Porrello A.M. Death and Denial: The Failure of the Therac-25, A Medical Linear Accelerator. |
| 4. | Leveson N.G., Clark S.T. An Investigation of the Therac-25 Accidents // Computer. July, 1993. P. 18-41. |
| 5. | Patriot missile defense: Software problems led to system failure at Dhahran, Saudi Arabia. Report GAO/IMTEC-92-26, Information Management and Technology Division, US General Accounting Office. Washington DC, Feb. 11992. |
| 6. | Berry D. M. Formal methods: the very idea, some thoughts about why they work when they work. // Science of Computer Programming #42(1). P. 11-27. |
| 7. | Floyd R. W. Assigning meanings to programs // Proceedings Symp. Appl. Math., 19. in: J.T.Schwartz (ed.), Mathematical Aspects of Computer Science. P. 19-32. American Mathematical Society, Providence, R.I., 1967. |
| 8. | Francez N. Verification of programs. Addison-Wesley Publishers Ltd., 1992. |
| 9. | Manna Z. Mathematical theory of computation. McGraw-Hill, 1974. |
| 10. | Manna Z., Pnueli A. The Temporal Logic of Reactive and Concurrent Systems. Springer-Verlag, 1991. |
| 11. | Blackburn M., Busser R., Nauman A., Knockerbocker R., Kasuda R. Mars Polar Lander Fault Identification Using Model-Based Testing // 26th Annual NASA Goddard Software Engineering Workshop. 27-29 November, 2001. |
| 12. | Dalal S. R., Jain A., Karunanithi N., Leaton J. M., Lott C. M. Model-Based Testing of a Highly Programmable System // Proceedings of ISSRE-98. 5-7 November 1998. |
| 13. | Dalal S. R., Jain A., Karunanithi N., Leaton J. M., Lott C. M., Patton G. C., Horowitz B. M. Model-Based Testing in Practice // Proceedings of the ICSE'99. May 1999. |
| 14. | Farchi E., Hartman A., Pinter S. S. Using a Model-Based Test Generator to Test for Standard Conformance // IBM Systems Journal, 2002. V. 41, No. 1, P. 89-110. |
| 15. | Gronau A., Hartman A., Kirshin A., Nagin K., Olvovsky S. A Methodology and Architecture for Automated Software Testing // IBM Research Laboratory in Haifa Technical Report, 2000. |
| 16. | Offutt A. J., Liu S., Abdurazik A. Generating Test Data from State-Based Specifications // Journal of Software Testing, Verification & Reliability. V. 13, No. 1, March 2003. |
| 17. | Al-Ghafees M., Whittaker J. A. Markov Chain-based Test Data Adequacy Criteria: a Complete Family. // IS June 2002. P. 13-37. |
| 18. | Bourdonov I., Kossatchev A., Kuliamin V., Petrenko A. UniTesK Test Suite Architecture // Proceedings of FME, 2002. LNCS 2391. P. 77-88. Springer-Verlag. |
| 19. | Кулямин В.В., Петренко А.К., Косачев А.С., Бурдонов И.Б. Подход UniTesK к разработке тестов // Программирование, 29(6). 2003. С. 25-43. |
| 20. | Баранцев А.В., Бурдонов И.Б., Демаков А.В., Зеленов С.В., Косачев А.С., Кулямин В.В., Омельченко В.А., Пакулин Н.В., Петренко А.К., Хорошилов А.В. Подход UniTesK к разработке тестов: достижения и перспективы // Труды Института системного программирования РАН, №5, 2004. . |
| 21. | Meyer B. Applying 'Design by Contract' // IEEE Computer, vol. 25, October 1992. P. 40 51. |
| 22. | [,PDF]. |
| 23. | Burdonov I., Kossatchev A., Petrenko A., Cheng S., Wong H. Formal Specification and Verification of SOS Kernel // BNR, NORTEL Design Forum, June 1996. |
| 24. | Monin J. F., Hinchey M. G. Understanding Formal Methods. Springer-Verlag, 2003. |
| 25. | Бурдонов И.Б., Косачев А.С., Кулямин В.В. Использование конечных автоматов для тестирования программ. // Программирование, 2000, №2. |
| 26. | Бурдонов И.Б., Косачев А.С., Кулямин В.В. Неизбыточные алгоритмы обхода ориентированных графов. Детерминированный случай. // Программирование. 2003. №5. С. 11 30. |
| 27. | Бурдонов И.Б., Косачев А.С., Кулямин В.В. Неизбыточные алгоритмы обхода ориентированных графов. Недетерминированный случай. // Программирование. 2004. №1. С. 4 24. |
| 28. | Бурдонов И.Б., Косачев А.С., Кулямин В.В. Асинхронные автоматы: классификация и тестирование. // Труды ИСП РАН. 2003. №4. С. 7 84. |
| 29. | Хорошилов А.В. Спецификация и тестирование компонентов с асинхронным интерфейсом. Диссертация на соискание ученой степени кандидата физико-математических наук. Москва, ИСП РАН, 2006. |
| 30. | Липский В. Комбинаторика для программистов. Москва, Мир, 1988. |
| 31. | Message Sequence Charts. ITU recommendation Z.120. |
| 32. | Agamirzian I., Groshev S.G., Khoroshilov A.V., Kluchnikov G.N., Kossatchev A.S., Omelchenko V.A., Pakoulin N.V., Petrenko A.K., Shnitman V.Z. MSR IPv6 verification project, December 2001. []. |
| 33. | Agamirzian I., Groshev S.G., Khoroshilov A.V., Kluchnikov G.N., Kossatchev A.S., Omelchenko V.A., Pakoulin N.V., Petrenko A.K., Shnitman V.Z. MSR IPv6 Verification within the CTesK-lite Framework, April 2002. []. |
| 34. | []. |
| 35. | Linux Standard Base Core 3.1. ISO/IEC IS-23360. []. |
| 1(обратно к тексту) | В данной работе рассматриваются только не более чем счетные множества. |
| 2(обратно к тексту) | Здесь под процессом тестирования понимается процесс выполнения уже разработанного теста. Если под процессом тестирования понимать процесс разработки теста, то данное утверждение будет не совсем верно. |
| 3(обратно к тексту) | Данные правила приводятся только для целей иллюстрации, поэтому их определение дано на поверхностном уровне, не рассматриваются вопросы, касающиеся области их применимости, и т.д. |
| 4(обратно к тексту) | Множества Xstack, Ystack и Vstack определяются с точностью до изоморфизма. |
| 5(обратно к тексту) | В указанной работе этот алгоритм обозначается символом A2. |
| 6(обратно к тексту) | Определение обозначений XI, YI и VI смотрите в разделе "Описание модели требований". |
| 7(обратно к тексту) | Более детальное обсуждение проблемы нарушения предусловия интерфейсных операций-стимулов смотрите в разделе "Нарушение предусловий асинхронных воздействий". |
| 8(обратно к тексту) | Здесь и далее идентификатор Unit будет обозначать множество, состоящее из единственного элемента e, а идентификатор Bool - множество, состоящее из двух элементов true и false. |
| 9(обратно к тексту) | В рамках данного доказательства мы считаем, что ei = ( vi, xi, v'i ). |
Механизм построения тестового сценария dfsm
Основным механизмом построения тестовых сценариев в технологии UniTesK является механизм построения тестового сценария dfsm. Этот механизм основан на неизбыточном алгоритме обхода на классе детерминированных сильно-связных конечных ориентированных графов αdfsm, представленном в работе [].
Тестовым сценарием dfsm для целевой системы с интерфейсом ( X, Y, V ) называется автоматный тестовый сценарий со сценарными функциями, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αdfsm.
Механизмом построения тестового сценария dfsm называется функция, преобразующая тестовый сценарий dfsm в тестовый сценарий посредством применения автоматного механизма сценарных функций.
Как показано в [], любое конечное функционирование тестового сценария dfsm приводит
либо к обнаружению нарушения требований детерминированности или сильно-связности графа сценария, либо к построению обхода этого графа.
С другой стороны, бесконечное функционирование тестового сценария dfsm возможно только в случае бесконечности графа сценария, или в случае бесконечного функционирования одной из сценарных функций.
Таким образом, если поведение целевой системы удовлетворяет требованиям, то при выполнении следующих условий
граф сценария при любом корректном функционировании целевой системы является детерминированным и сильно-связным; всякая сценарная функция при любом корректном функционировании целевой системы завершается за конечное число шагов;
тестовый сценарий dfsm завершает свою работу и путь, пройденный по графу сценария, является обходом этого графа.
Метрики покрытия асинхронной модели требований
Метрикой покрытия асинхронной модели требований A = ( V, X, Y, Z, E ) называется конечное множество подмножеств переходов модели требований M

Частично-упорядоченное множество ( P',


множество P' является подмножеством P ( P'








(p1,p2)









(p1,p2)






Предположим, что асинхронный тест ( P,




( P',





( P'',





Заметим, что всякое максимальное успешное префиксное подмножество асинхронного теста ( P,

Если асинхронный тест ( P,


Если асинхронный тест ( P,





Метрики покрытия модели требований
Метрикой покрытия модели требований A = ( V, X, Y, E ) называется конечное множество подмножеств переходов модели требований M

Будем говорить, что тест { ( vi, xi, yi, v'i ) } покрыл элемент покрытия Cj

Таким образом, метрика покрытия определяет конечный набор элементов, в терминах которых осуществляется оценка качества тестирования. В технологии UniTesK некоторые метрики генерируются автоматически на основе структуры постусловий интерфейсных функций. В дополнение к этим метрикам, разработчик тестов может определять свои собственные метрики покрытия. Тестовая система автоматически оценивает качество тестирования в терминах всех доступных метрик и по результатам теста генерирует отчеты о покрытии элементов каждой метрики.
Метрика покрытия M называется управляемой, если для любых двух взаимодействий I1 = ( v1, x1, y1, v'1 ) и I2 = ( v2, x2, y2, v'2 ) выполнено следующее утверждение: (v1 = v2)







Для управляемых метрик характерно то, что принадлежность взаимодействия к тому или иному элементу покрытия зависит только от той части взаимодействия, которая управляется тестовой системой, то есть от пресостояния и стимула. Работая с управляемыми метриками, тестовая система может не только автоматически подсчитывать их покрытие, но и оптимизировать генерацию тестовых данных для достижения определенного покрытия по некоторой управляемой метрике.
Метрики покрытия в унифицированной архитектуре теста
В процессе тестирования, при вызове интерфейсной операции, тестовая система вычисляет для каждой метрики, заданной для данной операции, все элементы покрытия, покрытые данным вызовом. Информация о покрытых элементах попадает в трассу теста. По трассе одного или нескольких тестов генерируются отчеты о покрытии интерфейсных операций, согласно определенным для них метрикам покрытия.
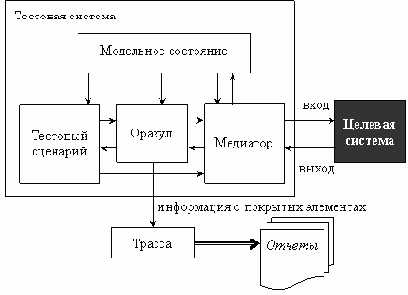
Рисунок 8.Универсальная архитектура теста с учетом оценки качества тестирования
Компонент тестовой системы, который отвечает за вычисление покрытых элементов в рамках одного вызова интерфейсной операции, - оракул. Он обладает всей информацией, необходимой для выполнения этого действия. Для известных ему пресостояния, стимула, реакции и постсостояния оракул вычисляет покрытые элементы и помещает результат вычисления в трассу. Для метрики покрытия, описанной функцией μ, оракул вычисляет значение этой функции, которое однозначно характеризует покрытый элемент. Для расширенной метрики покрытия оракул вычисляет значения всех предикатов ci и индексы предикатов, принявших положительное значение, помещаются в трассу в качестве описания покрытых элементов.
Помимо информации о покрытых элементах в трассу попадает информация о вызовах интерфейсных операций, значениях их параметров, вердиктах оракула, а также о других событиях, произошедших в процессе тестирования. По завершении процесса тестирования трасса используется для анализа результатов тестирования. На ее основе генерируются отчеты о покрытии, отчеты о найденных несоответствиях между поведением целевой системы и требованиями к нему, а также отчеты об ошибках, имевших место в тестовой системе. Архитектура тестовой системы, дополненная работой с метриками покрытия, представлена на .
Модель каналов
Модель каналов предназначена для задания частичного порядка на наборе асинхронных взаимодействий.
Определение 10.
Пусть D - конечное или бесконечное множество. Моделью каналов на множестве D мы будем называть конечное или бесконечное множество упорядоченных подмножеств множества D Ch = { ( Di, <i ) | i = 1, …, n, … }, такое что
подмножества Di взаимно не пересекаются (



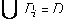
Модель каналов задает частичный порядок на множестве D, определяемый следующим образом:
d1



Множества Di модели каналов мы будем называть каналами.
Модель каналов во многих случаях является удобным механизмом для задания частичного порядка, так как она позволяет описывать наиболее естественным способом порядок взаимодействий, происходивших в одном "канале".
Например, если сетевой протокол, с помощью которого осуществляется взаимодействие, обеспечивает сохранение порядка сообщений, то все сообщения посылаемые через один "сокет" на другой "сокет" между собой строго упорядочены. Тем не менее, никакой информации о порядке доставки этих сообщений относительно сообщений, посылаемых по другим парам "сокетов", не известно.
В таких ситуациях, модель каналов позволяет отнести все упорядоченные сообщения к одному каналу и задать для этого канала соответствующий порядок. Чтобы сделать это, при регистрации каждого взаимодействия в тестовой системе предлагается указывать в качестве одной из характеристик взаимодействия - идентификатор канала, к которому относится данное взаимодействие. Порядок взаимодействий в рамках одного канала задается порядком регистрации взаимодействий. Считается, что взаимодействие, которое было зарегистрировано раньше другого, относящегося к тому же каналу, произошло раньше, чем второе.
Но одной модели каналов оказывается недостаточно для описания произвольного частичного порядка. Поэтому существует еще один механизм для определения частичного порядка на асинхронной модели поведения целевой системы.
Модель поведения
Интерфейсом целевой системы будем называть тройку ( X, Y, V ), где
X - множество стимулов, Y - множество реакций, V - множество состояний.
Каждое из этих множеств может быть бесконечным . Взаимодействием с целевой системой, обладающей интерфейсом ( X, Y, V ), будем называть четверку ( v, x, y, v' )

Понятие взаимодействия можно интерпретировать следующим образом. В состоянии v вызывается интерфейсная операция с некоторыми значениями параметров x, на что целевая система возвращает выходные параметры y и переходит в состояние, соответствующее состоянию v'.
Например, для функции вычисления квадратного корня возможны следующие взаимодействия: ( ε, sqrt( 0.0 ), 0.0, ε ), ( ε, sqrt( 4.0 ), 2.0, ε ) или ( ε, sqrt( 10.0 ), 1.0, ε ). В этом примере множество состояний V состоит из единственного элемента ε, множество стимулов X и реакций Y совпадают с множеством всех неотрицательных действительных чисел.
Определение 1.
Моделью поведения целевой системы с интерфейсом ( X, Y, V ) будем называть конечное или бесконечное мультимножество взаимодействий { ( vi, xi, yi, v'i ) }.
Модель поведения соответствует набору взаимодействий с целевой системой, имевших место в процессе тестирования. Например, предположим, что в процессе тестирования функция вычисления квадратного корня была вызвана трижды с параметрами 0.0, 4.0 и 10.0 и вернула значения 0.0, 2.0 и 1.0 соответственно. Тогда моделью поведения целевой системы будет мультимножество взаимодействий, произошедших в процессе тестирования { ( ε, sqrt( 0.0 ), 0.0, ε ), ( ε, sqrt( 4.0 ), 2.0, ε ), ( ε, sqrt( 10.0 ), 1.0, ε ) }.
Второй класс асинхронных взаимодействий содержит взаимодействия, инициируемые целевой системой. Такие взаимодействия мы называем асинхронными реакциями (или отложенными реакциями). Асинхронные реакции используются для моделирования данных передаваемых только в направлении от целевой системы.
Таким образом, моделировать взаимодействия с целевой системой предлагается следующим способом. Если взаимодействие инициируется окружением целевой системы, то для его описания используются асинхронные воздействия. При этом данные, передаваемые в направлении к целевой системе, описываются стимулом, а данные, передаваемые от целевой системы, описываются непосредственной реакцией.
Если взаимодействие инициируется целевой системой и данные в рамках этого взаимодействия передаются только в направлении от целевой системы, то такие взаимодействия моделируются асинхронными реакциями.
Если же взаимодействие инициируется целевой системой, но данные в рамках этого взаимодействия передаются и от целевой системы, и к ней, то при моделировании таких взаимодействий предлагается разбивать их на меньшие составляющие, которые описываются посредством асинхронных воздействий и асинхронных реакций. Например, такое взаимодействие можно разбить на асинхронную реакцию, инициируемую целевой системой, и на набор последующих асинхронных воздействий, включающих в себя данные, передаваемые к целевой системе.
| 1 | Окружение целевой системы | к целевой системе и от нее | Асинхронное воздействие |
| 2 | Целевая система | только от целевой системы | Асинхронная реакция |
| 3 | Целевая система | от целевой системы и к ней | Асинхронная реакция и последующие асинхронные воздействия |
Суммарная информация по предлагаемым способам моделирования взаимодействий целевой системы с ее окружением представлена в таблице 1.
Определение 7.
Асинхронной моделью поведения целевой системы с интерфейсом ( X, Y, Z ) называется частично-упорядоченное мультимножество асинхронных взаимодействий ( P,

Модель поведения состоит из, возможно, бесконечного набора асинхронных взаимодействий, имевших место в процессе тестирования. Частичный порядок, заданный на этом наборе, определяет, в каком порядке происходили взаимодействия. p1

Множество всех асинхронных моделей поведения целевой системы с интерфейсом ( X, Y, Z ) мы будем обозначать Ω( X, Y, Z ).
Модель требований
Абстрактным автоматом будем называть четверку ( V, X, Y, E ), где
V - множество состояний, X - множество стимулов, Y - множество реакций, E

Переходы автомата ( v, x, y, v' ) состоят из пресостояния v, стимула x, реакции y и постсостояния v'. Множества V, X, Y и E могут быть бесконечными.
Определение 2.
Моделью требований к целевой системе с интерфейсом ( X, Y, V ) будем называть абстрактный автомат, множества состояний, стимулов и реакций которого совпадают с V, X и Y соответственно.
Будем говорить, что взаимодействие ( v, x, y, v' ) является корректным относительно модели требований A = ( V, X, Y, E ), если оно принадлежит множеству переходов E.
Будем говорить, что модель поведения целевой системы { ( vi, xi, yi, v'i ) } удовлетворяет модели требований A = ( V, X, Y, E ), если


Рассмотрим пример с функцией вычисления квадратного корня. Что является моделью требований к этой функции? Интерфейс этой системы ( X, Y, V ) был определен в предыдущем разделе. Множество переходов E определим как все переходы ( ε, x, y, ε )

Другими словами, асинхронная модель поведения удовлетворяет модели требований с данным начальным состоянием, если взаимодействия из мультимножества P можно упорядочить, не вступая в противоречие с частичным порядком

Важно отметить, что асинхронная модель требований предполагают, что для любого набора взаимодействий, осуществлявшихся параллельно, существует эквивалентное с точки зрения конечного результата последовательное выполнение этих взаимодействий. Если данная гипотеза, называемая гипотезой простого параллелизма [], не выполняется, то необходимо разбить взаимодействия на более мелкие, для которых гипотеза будет верна. Если никакое разбиение не позволяет добиться выполнения данной гипотезы, то рассматриваемый метод является неприменимым для тестирования такой системы. На настоящий момент автору неизвестен пример программной системы, для которой невозможно выбрать асинхронный интерфейс, удовлетворяющий гипотезе простого параллелизма.
Проверка наличия отношения "удовлетворяет" для асинхронных моделей значительно сложнее, по сравнению с синхронным случаем. Поэтому необходимо провести дополнительный анализ алгоритма этой проверки. Но прежде чем рассматривать этот алгоритм, мы остановимся на способах описания модели требований и модели поведения, так как способы задания моделей оказывают существенное влияния на алгоритмы работы с ними.
Модель временных меток
Модель временных меток предназначена для возможности задания дополнительных ограничений на порядок взаимодействий в асинхронной модели поведения целевой системы.
Пусть ( TM,



Множество всех временных интервалов будет обозначаться TI(TM). Определим на нем частичный порядок

( tm1, tm2 )



Определение 11.
Пусть D - конечное или бесконечное множество, а ( TM,


Модель временных меток задает на множестве D частичный порядок

d1



В качестве множества временных меток TM в технологии UniTesK используется множество (F x Nat)

Для описания частичного порядка






















Для установки зависимостей последнего типа тестовая система предоставляет специальную функцию, с помощью которой в процессе тестирования можно зафиксировать зависимости между временными метками. Множество систем координат F также определяется динамически, в процессе тестирования.
Модель временных меток предоставляет удобный способ для описания частичного порядка на множестве взаимодействий при использовании в следующей интерпретации.
Временная метка рассматривается как идентификатор некоторого момента времени. Каждый момент времени описывается натуральным числом в некоторой системе временных координат. В рамках одной системы координат все моменты времени упорядочены. А про моменты времени, принадлежащие различным системам координат, заранее ничего не известно. Но если какая-нибудь информация появляется, то она фиксируется согласно четвертому правилу.
Каждому взаимодействию ставится в соответствие временной интервал, первая временная метка, которого описывает момент начала взаимодействия, а вторая - момент его завершения. Таким образом, считается, что одно взаимодействие достоверно произошло раньше другого, если временная метка завершения первого взаимодействия меньше временной метки начала второго. В качестве концов интервала допускается использование специальных значений -∞ и +∞, предназначенных для описания открытых интервалов.
Способ выделения натуральных чисел, используемых для описания момента времени, может варьироваться. Это может быть текущее значение системного таймера или просто некоторое абстрактное число. Различные системы временных координат, например, могут соответствовать различным машинам в сети.
Определять модель временных меток предлагается следующим образом. Во-первых, в процессе тестирования фиксируется информация об отношении порядка между временными метками, принадлежащими различным системам координат. А во-вторых, при регистрации взаимодействий указывается временной интервал, соответствующий данному взаимодействию.
Модели требований и поведения в унифицированной архитектуре теста
Унифицированная архитектура теста определяет набор компонентов тестовой системы, область ответственности каждого компонента, а также основные правила взаимодействия этих компонентов. В данном разделе мы рассмотрим унифицированную архитектура теста, в той ее части, которая связана с оценкой корректности поведения целевой системы.
В технологии UniTesK поведение целевой системы рассматривается как набор отдельных, не связанных между собой взаимодействий. Соответственно, задача оценки корректности поведения целевой системы декомпозируется на частные задачи оценки корректности отдельных взаимодействий.
За оценку корректности взаимодействий отвечает специальный компонент тестовой системы - оракул. Этот компонент генерируется автоматически на основе описания модели требований в виде спецификации целевой системы. Модель поведения целевой системы строится динамически и за это отвечает другой компонент тестовой системы - медиатор. Оракул и медиатор являются одними из основных элементов унифицированной архитектуры теста. Рассмотрим их подробнее.
Медиаторы отвечают в тестовой системе за всю работу с целевой системой. Основными задачами медиатора являются оказание тестового воздействия на целевую систему и построение модели поведения целевой системы. Эти задачи тесно связаны, так как в синхронном случае любое взаимодействие начинается с оказания тестового воздействия или стимула. Ответная реакция целевой системы является другой составляющей взаимодействия. Кроме этого, взаимодействие характеризуется пресостоянием и постсостоянием.
Унифицированная архитектура теста предполагает неявное построение пресостояния и постсостояния. Тестовая система содержит модельное состояние, в котором хранятся текущие значения переменных состояния, определенных в спецификации целевой системы. Соответственно, значения переменных состояния, хранящиеся в модельном состоянии до оказания стимула, считаются пресостоянием, а значения этих переменных после оказания стимула - постсостоянием. За синхронизацию модельного состояния с внутренним состоянием целевой системы отвечает медиатор.
Исходя из этого, работа медиатора строится по следующему алгоритму. Получив указание подать стимул x


В некоторых случаях значения переменных модельного состояния могут быть вычислены на основе достоверных знаний о внутреннем состоянии тестируемой системы. Тогда тестовая система может во время тестирования не только проверять требования к внешнему поведению целевой системы, но и контролировать ее внутреннее состояние. Это позволяет упростить локализации ошибок, так как некорректное изменение внутреннего состояния одной интерфейсной операцией может проявиться на внешнем поведении целевой системы только после многих вызовов других операций.
Тестирование с использованием достоверных знаний о внутреннем состоянии целевой системы называется тестированием с открытым состоянием. В противном случае, тестирование называется тестированием со скрытым состоянием. Технология UniTesK поддерживает оба этих подхода.
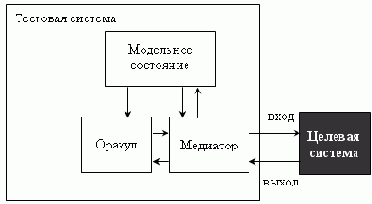
Рисунок 3.Механизм работы оракула и медиатора
При тестировании с открытым состоянием медиатор вычисляет модельное состояние непосредственно на основе знаний о внутреннем состоянии целевой системы. Если при тестировании системы, реализующей функциональность целочисленного стека, медиатор читает текущее состояние стека, не используя тестируемые функции, то это пример тестирования с открытым состоянием.
Если же доступ к внутреннему состоянию невозможен, то модельное состояние вычисляется, исходя из предположения о корректном поведении целевой системы и дополнительных знаний о ее реализации. В примере со стеком медиатор может не иметь доступа к текущему состоянию стека и тогда он будет вынужден вычислять это состояние, основываясь на предположении, что целевая система работает корректно.
Если требования к целевой системе определяют единственное постсостояние, для данных пресостояния, стимула и реакции, то проблем с неопределенностью модельного состояния после оказания тестового воздействия не возникает. В противном случае, в медиаторах необходимо использовать дополнительные знания о конкретной реализации, чтобы правильно вычислить текущее модельное постсостояние.
Согласно унифицированной архитектуре теста основным потребителем сервисов, предоставляемых медиатором, является оракул. Именно он просит медиатор подать стимул x и получает от него реакцию y. Задача оракула заключается в оценке корректности отдельного взаимодействия с целевой системой относительно модели требований.
Технически работа оракулов организована следующим образом. Оракул запоминает все необходимые части текущего модельного состояния v и передает стимул x медиатору. Медиатор оказывает тестовое воздействие, моделируемое посредством стимула x, получает реакцию целевой системы, преобразует ее в модельное представление y и синхронизирует текущее модельное состояние с внутренним состоянием реализации. Оракул, зная сохраненное состояние v, стимул x, реакцию y и текущее состояние v', выносит вердикт о корректности данного взаимодействия.
Оракул генерируется автоматически на основе описания модели требований в терминах предусловий и постусловий интерфейсных операций. Медиатор описывается разработчиком тестов вручную или с помощью техники шаблонов.
Часть архитектуры тестовой системы, разработанной согласно технологии UniTesK, связанная с организацией взаимодействия между медиатором и оракулом представлена на . Здесь стрелками обозначены направления передачи данных между компонентами тестовой системы.
На рисунках и представлены диаграммы взаимодействия UML, иллюстрирующие основные варианты работы этой части тестовой системы при тестировании с открытым и со скрытым состоянием соответственно. Работа оракула начинается с получения указания осуществить тестовое воздействие, моделируемое посредством стимула x.От кого именно поступает данное указание, в настоящий момент не рассматривается. Дальнейшая последовательность взаимодействий оракула, медиатора и целевой системы происходит так, как рассматривалось ранее.
Если требования к целевой системе определяют единственное постсостояние, для данных пресостояния, стимула и реакции, то проблем с неопределенностью модельного состояния после оказания тестового воздействия не возникает. В противном случае, в медиаторах необходимо использовать дополнительные знания о конкретной реализации, чтобы правильно вычислить текущее модельное постсостояние.
Согласно унифицированной архитектуре теста основным потребителем сервисов, предоставляемых медиатором, является оракул. Именно он просит медиатор подать стимул x и получает от него реакцию y. Задача оракула заключается в оценке корректности отдельного взаимодействия с целевой системой относительно модели требований.
Технически работа оракулов организована следующим образом. Оракул запоминает все необходимые части текущего модельного состояния v и передает стимул x медиатору. Медиатор оказывает тестовое воздействие, моделируемое посредством стимула x, получает реакцию целевой системы, преобразует ее в модельное представление y и синхронизирует текущее модельное состояние с внутренним состоянием реализации. Оракул, зная сохраненное состояние v, стимул x, реакцию y и текущее состояние v', выносит вердикт о корректности данного взаимодействия.
Оракул генерируется автоматически на основе описания модели требований в терминах предусловий и постусловий интерфейсных операций. Медиатор описывается разработчиком тестов вручную или с помощью техники шаблонов.
Часть архитектуры тестовой системы, разработанной согласно технологии UniTesK, связанная с организацией взаимодействия между медиатором и оракулом представлена на . Здесь стрелками обозначены направления передачи данных между компонентами тестовой системы.
На рисунках и представлены диаграммы взаимодействия UML, иллюстрирующие основные варианты работы этой части тестовой системы при тестировании с открытым и со скрытым состоянием соответственно. Работа оракула начинается с получения указания осуществить тестовое воздействие, моделируемое посредством стимула x.От кого именно поступает данное указание, в настоящий момент не рассматривается. Дальнейшая последовательность взаимодействий оракула, медиатора и целевой системы происходит так, как рассматривалось ранее.
Оно используется только в модели требований для определения корректности поведения.
В алгоритме оценки корректности поведения функция γ описывает множество допустимых модельных состояний после данного взаимодействия при заданном начальном состоянии системы. Модель требований может допускать большое количество таких состояний, абстрагируясь от деталей реализации описываемых требований. Анализ всех этих состояний может требовать большого количества ресурсов. В то же время, при тестировании конкретной целевой системы может быть известно о деталях поведения данной реализации, на основе которых можно ограничить множество допустимых модельных состояний только теми состояниями, которые будут соответствовать корректному поведению данной реализации. Так как такое ограничение является реализационнозависимым, то оно описывается в медиаторе, а именно в специальном компоненте медиатора, называемом медиатором состояния. Подробнее, назначение медиатора состояния будет рассмотрено при обсуждении работы оракула.

Рисунок 12. Медиатор в универсальной архитектуре асинхронного теста
Устройство медиатора, предназначенного для тестирования асинхронных систем, представлено на рисунке 12. Как и ранее, стрелками здесь обозначены направления передачи данных между компонентами тестовой системы.
Оракул решает задачу оценки корректности поведения тестируемой системы в ходе работы теста. Алгоритм решения этой задачи был представлен в предыдущем разделе. Он учитывает в своей работе все имевшие место взаимодействия с тестируемой системой и связи между ними. Поэтому компонент оракула, реализующий этот алгоритм, мы будем называть гипероракулом. Гипероракул получает от регистратора взаимодействий информацию обо всех взаимодействиях, зарегистрированных в процессе работы теста, и дальше действует согласно алгоритму оценки корректности поведения.
Алгоритм оценки корректности поведения предполагает, что модель требований задана посредством функции γ : V x ( (X x Y)



Это множество может быть шире множества допустимых состояний, вычисленных γ'' с учетом дополнительных требований. Но только за счет состояний, не удовлетворяющих исходной модели требований.





γ''( v, p )




В простейшем случае, при отсутствии уточнения требований, функция γ* совпадает с функцией подсказки γ'.
Далее мы будем считать, что размерность множества γ*( v, p ) не превышает 1. Это требование является ограничением на область применимости архитектуры. Заметим, что данное ограничение выполняется для всех детерминированных моделей требований и, кроме того, оно выполняется для недетерминированных моделей требований, если требования к тестируемой реализации могут быть уточнены до достижения детерминированности.
Итак, гипероракул вычисляет вместо функции γ ее модификацию γ''( v, p ), и это вычисление происходит следующим образом:
Гипероракул устанавливает модельное состояние равным v. Гипероракул вызывает оракул воздействия для взаимодействия p. Оракул воздействия вычисляет предусловие взаимодействия p: preS



Моделирование требований и поведения
Вопрос построения моделей требований и поведения является очень непростым, как и всякий вопрос, связанный с переходом от неформальной сущности к формальной модели. Для целого ряда частных случаев можно представить правила и рекомендации по построению моделей. Тем не менее, в общем случае решение этой задачи во многом основывается на опыте и интуиции разработчика тестов.
Для иллюстрации взаимосвязи моделей требований и поведения с реальными объектами, рассмотрим один из вариантов построения этих моделей в том случае, когда целевая система представляет собой систему с прикладным программным интерфейсом.
Предположим, что целевая система предоставляет своим пользователям прикладной программный интерфейс, состоящий из n функций. Каждая интерфейсная функция имеет набор входных и выходных параметров. Кроме того, вызов интерфейсных функций может изменять внутреннее состояние целевой системы или ее окружение, и таким образом влиять на результаты следующих вызовов интерфейсных функций.
Тогда для каждой функции прикладного интерфейса можно определить соответствующую ей интерфейсную операцию. Сигнатура интерфейсной операции определяется по следующим правилам:
входные параметры интерфейсной операции и их типы соответствуют входным параметрам функции прикладного интерфейса, выходные параметры интерфейсной операции и их типы соответствуют выходным параметрам функции прикладного интерфейса, переменные состояния соответствуют тем частям внутреннего состояния целевой системы и/или ее окружения, от которого зависит ожидаемое поведение функции прикладного интерфейса. Мы здесь использовали слово "ожидаемое", чтобы отметить, что в данном случае нас интересует поведение не конкретной реализации целевой системы, а поведение ожидаемое от нее пользователем.
Требования к поведению целевой системы после вызова функции прикладного интерфейса описывается в виде спецификации соответствующей интерфейсной операции. Таким образом, мы задаем модель требований к целевой системе посредством спецификации, состоящей из спецификаций отдельных интерфейсных операций.
Определив сигнатуры интерфейсных операций, участвующих в спецификации, мы тем самым определили интерфейс целевой системы ( X, Y, V ). Согласно MR[Spec] этот интерфейс определяется следующим образом:
множество стимулов X состоит из вызовов функций прикладного интерфейса со всеми допустимыми наборами входных параметров, множество реакций Y состоит из всех возможных возвращаемых значений интерфейсных функций, где под возвращаемым значением подразумевается кортеж значений выходных параметров данной функции, множество состояний V состоит из значений, соответствующих различным значениям внутреннего состояния целевой системы и/или ее окружения. При этом учитываются только те значения, от которых зависит ожидаемое поведение хотя бы одной функции прикладного интерфейса.
Взаимодействием с целевой системой в этом случае является четверка ( v, x, y, v' ), в которой:
пресостояние v соответствует состоянию целевой системы и/или ее окружения до вызова функции прикладного интерфейса, стимул x соответствует вызову функции прикладного интерфейса с определенным набором значений входных параметров, реакция y соответствует набору значений выходных параметров, который вернула вызванная функция, постсостояние v' соответствует состоянию целевой системы и/или ее окружения, в котором она оказалась после данного вызова.
Соответственно, модель поведения целевой системы состоит из множества таких четверок и строится тестовой системой в ходе тестирования.
Рассмотрим данный подход на примере системы, реализующей функциональность целочисленного стека. Прикладной программный интерфейс этой системы состоит из трех функций:
функция помещения числа в стек имеет один входной параметр - число, и не имеет выходных параметров, функция выборки элемента с вершины стека не имеет входных параметров и имеет один выходной параметр - число, находящееся на вершине стека, функция получения размера стека не имеет входных параметров и имеет один выходной параметр - число, равное текущему размеру стека.
Для определенности будем считать, что целые числа, участвующие в этом примере, заданы множеством Int.
Для каждой функции прикладного программного интерфейса определим соответствующую ей интерфейсную операцию.
Сигнатуру операции помещения числа в стек определим как ( { x }, {}, { vstack } ), где тип входного параметра x - Int, а переменной состояния vstack - Int-list. Спецификацию этой операции ( prepush, postpush ) зададим следующими предикатами:
prepush ( vstack, x ) ≡ true
postpush ( vstack, x, vstack' ) ≡ ( vstack' =


Сигнатуру операции выборки элемента с вершины стека определим как ( {}, { y }, { vstack } ), где тип выходного параметра y - Int, а переменной состояния vstack - Int-list. Спецификацию этой операции ( prepop, postpop ) зададим следующими предикатами:
prepop ( vstack, y ) ≡ size( vstack ) > 0
postpop ( vstack, y, vstack' ) ≡ ( y = head( vstack ) )

Сигнатуру операции получения размера стека определим как ( {}, { y }, { vstack } ), где тип выходного параметра y - Int, а переменной состояния vstack - Int-list. Спецификацию этой операции ( presize, postsize ) зададим следующими предикатами:
presize ( vstack, y ) ≡ true
postsize ( vstack, y, vstack' ) ≡ ( y = size( vstack ) )

Спецификации этих трех операций составляют спецификацию системы, реализующей функциональность целочисленного стека. На основе данной спецификации мы можем построить модель требований, как это определено в MR[Spec]. Наиболее важным для нас является интерфейс целевой системы, который определяется неявным образом при построении модели требований.
В данном случае интерфейс целевой системы есть ( Xstack, Ystack, Vstack ), где:
Xstack = Int




Рассмотрим, как будет выглядеть модель поведения целевой системы для одного из частных случаев. Предположим, что в ходе тестирования мы вызвали целевую систему четыре раза:
вызвали функцию помещения числа в стек с параметром 0, когда стек был пустым, и получили стек, содержащий число 0; вызвали функцию получения размера стека и получили 1, в качестве значения выходного параметра, значение стека не изменилось; вызвали функцию выборки элемента с вершины стека и получили 0, в качестве значения выходного параметра, значение стека не изменилось; вызвали функцию получения размера стека и получили 1, в качестве значения выходного параметра, значение стека не изменилось.
Модель поведения для данного теста будет состоять из четырех взаимодействий:
{
(




(




(




(




}
Если описать эту модель в терминах спецификации целевой системы, то мы получим следующее:
{
( vstack




( vstack




( vstack




( vstack




}
Пресостояние и постсостояние задается значением переменной состояния vstack, стимул записывается в виде идентификатора интерфейсной операции со списком значений ее входных параметров, а реакция - в виде идентификатора интерфейсной операции со списком значений ее выходных параметров.
Нарушение предусловий асинхронных воздействий
Для описания модели требований как синхронных, так и асинхронных систем используются спецификации интерфейсных операций. Каждая спецификация операции состоит из предусловия и постусловия. Предусловие описывает, какие значения входных параметров являются допустимыми в текущем модельном состоянии, а постусловие определяет какие значения выходных параметров и постсостояния модели являются корректными для данных значений входных параметров и пресостояния модели. Другими словами, предусловие описывает обязательства пользователя целевой системы перед этой системой, а постусловие - обязательства целевой системы перед своим пользователем.
В процессе тестирования синхронных систем, перед вызовом каждой интерфейсной операции, тестовая система проверяет предусловие этой операции на соответствующих значениях входных параметров. Таким образом, предотвращается возможность передачи целевой системе некорректных данных, которые могут привести к невозможности продолжать тестирование. Например, если в требованиях к целевой системе сказано, что ее поведение на некоторых входных данных не определено, а тестовая система вызвала интерфейсную операцию с такими значениями, то любое дальнейшее поведение целевой системы не будет противоречить требованиям к ней, и поэтому продолжать тестирование становится бессмысленно.
При тестировании асинхронных систем проверка предусловий интерфейсных операций существенно осложняется тем фактом, что в момент асинхронного взаимодействия тестовой системе может быть неизвестно текущее модельное состояние. Асинхронный тестовый сценарий может осуществлять несколько тестовых воздействий одновременно, получая в то же время отложенные реакции, и поэтому не владеть достоверной информацией о состоянии тестируемой системы в момент взаимодействия.
С другой стороны, в процессе оценки корректности поведения целевой системы становится доступной информация о возможном состоянии модели требований перед вызовом каждой операции. Причем таких состояний может быть несколько в зависимости от рассматриваемой линеаризации модели поведения.
Оценка качества тестирования
Мы рассмотрели, как работает тестовая система в масштабе одного взаимодействия с целевой системой и как организуется последовательность таких взаимодействий. При этом в тени осталась одна очень важная проблема, имеющая место в любом процессе тестирования - проблема оценка качества тестирования.
В подавляющем большинстве случаев проверить целевую систему на всех допустимых тестовых данных невозможно. Поэтому приходится ограничиваться некоторым конечным набором тестов. В такой ситуации неизбежно встает вопрос о качестве тестирования, проведенного посредством данного тестового набора.
Существует несколько подходов к решению этой задачи. Наиболее распространенный из них использует оценку качества на основе исходного кода целевой системы. Например, оценивается процент инструкций выполненных во время тестирования или процент покрытия возможных ветвлений потока управления.
Этот подход доказал свою важность и значимость. Однако, использование только оценки покрытия исходного кода применительно к функциональному тестированию часто оказывается недостаточным. Например, стопроцентное покрытие тестами исходного кода не гарантирует, что все требования к функциональности системы были надлежащим образом реализованы. Если какое-то требование было упущено и не нашло своего отражения в исходном коде, то тесты могут показывать идеальный процент покрытия, хотя в системе присутствует серьезный изъян.
С другой стороны, функциональное тестирование имеет своей целью проверить выполнение целевой системой требований, предъявляемых к ее функциональности. Поэтому измерение качества тестов, сформулированное в терминах этих требований, также является необходимым для получения адекватной оценки. Технология UniTesK предлагает именно такой подход, измерение качества тестирования в котором основывается на требованиях к функциональности системы.
Модель требований представляет собой абстрактный автомат A = ( V, X, Y, E ). Для оценки покрытия при тестировании конечных автоматов традиционно используются оценки числа покрытых состояний или переходов по сравнению с их общим числом. Но так как абстрактный автомат, как правило, является бесконечным, то такие методы оценки покрытия оказываются неприемлемыми. Для решения этой проблемы в технологии UniTesK используются метрики покрытия модели требований.
Оценка качества тестирования в унифицированной архитектуре асинхронного теста
Оценка качества тестирования асинхронных систем проводится по той же схеме, что и при тестировании синхронных систем. В процессе выполнения теста вычисляется принадлежность каждого отдельного перехода в асинхронной модели требований ко всем заданным разработчиком теста асинхронным метрикам покрытия. Эта информация сохраняется в трассе теста. И уже после завершения тестирования выполняется анализ трассы и генерация отчетов о покрытии асинхронных метрик покрытия.
В унифицированной архитектуре асинхронного теста за рассмотрение каждого отдельного перехода в асинхронной модели требований отвечает оракул воздействия. Поэтому именно на него накладывается дополнительная ответственность за вычисление принадлежности этого перехода к элементам метрик покрытия и помещение этой информации в трассу теста.
Если асинхронная метрика покрытия задана функцией μ, то оракул воздействия вычисляет значение этой функции и помещает его в трассу, так как оно однозначно характеризует покрытый элемент метрики. Если асинхронная метрика покрытия задана расширенной метрики покрытия, то оракул воздействия вычисляет значения всех предикатов ci и индексы предикатов, принявших положительное значение, помещаются в трассу в качестве описания покрытых элементов.
Но при тестировании систем с асинхронным интерфейсом информации о принадлежности отдельных переходов к элементам метрики недостаточно для определения покрытия этой метрики. Чтобы вычислить покрытие необходимо учитывать все успешные пути в модели требований, а также принадлежность переходов этим путям. Эта информация помещается в трассу теста гипероракулом, так как именно этот компонент тестовой системы управляет процессом линеаризации и обладает всеми необходимыми данными.
Принципы измерения покрытия асинхронных метрик в процессе тестирования представлены на . Гипероракул и оракул воздействия помещают информацию, необходимую для вычисления покрытия заданных пользователем асинхронных метрик покрытия, в трассу теста. В последствии трасса анализируется специальными инструментами, которые генерируют отчеты о качестве тестирования в терминах метрик покрытия асинхронной модели требований.
Оценка корректности поведения тестируемой системы
Технология UniTesK предназначена для автоматизации процесса разработки и выполнения функциональных тестов. При этом под функциональным тестированием понимается процесс взаимодействия с целевой системой, направленный на проверку выполнения этой системой требований, предъявляемых к ее функциональности. В этом определении два ключевых момента: взаимодействия и требования.
Типичным примером взаимодействия с тестируемой системой является вызов ее интерфейсной функции и получения результата ее работы. Другим примером взаимодействия может быть посылка HTTP запроса и получение ответа на этот запрос. То есть взаимодействием является любой обмен информацией с целевой системой, в том числе и направленный только в одну сторону.
Требования к функциональности целевой системы описывают ту функциональность, которую данная система должна предоставлять своему пользователю. Поскольку пользователь общается с целевой системой посредством взаимодействий, то и его требования к системе выражаются в терминах взаимодействий. Другими словами, требования определяют какие взаимодействия являются корректными (ожидаемыми), а какие - нет.
Например, пользователь библиотеки математических функций ожидает, что вызвав функцию sqrt с параметром x, он получит квадратный корень x, вычисленный с заданной точностью.
В настоящей работе под оценкой корректности поведения целевой системы понимается проверка того, что поведение целевой системы, наблюдаемое в процессе тестирования, удовлетворяет требованиям, предъявляемым к функциональности системы.
Описание асинхронной модели поведения
Суммируя информацию о построении асинхронной модели поведения целевой системы в процессе тестирования, можно сказать, что этот процесс состоит из решения двух задач:
регистрации взаимодействий, фиксирования достоверно известной информации о порядке, в котором происходили эти взаимодействия.
Регистрация взаимодействий осуществляется в специальном компоненте тестовой системы - регистраторе взаимодействий. А для решения второй задачи предлагается при регистрации взаимодействий указывать идентификатор канала, к которому относится данное взаимодействие, и временной интервал, в котором оно происходило. Кроме того, требуется фиксировать известные ограничения на порядок временных меток, принадлежащих различным системам координат.
В результате этого тестовая система будет иметь набор асинхронных взаимодействий D, модель каналов Ch и модель временных меток τ. На основе этой информации будет построена асинхронная модель поведения ( P,

мультимножество взаимодействий P совпадает с D, частичный порядок π является транзитивным замыканием объединения частичных порядков


Описание асинхронной модели требований
Для описания асинхронных моделей требований используется немного модифицированный подход программных контрактов. Основные идеи этого способа состоят в следующем.
Для целевой системы проводится анализ ее интерфейса. В ходе анализа выявляются виды взаимодействий, в которых целевая система может принимать участие, и их параметры. Для каждого вида определяется, кто является инициатором взаимодействия данного вида, и какие данные передаются в ходе взаимодействия по направлению к целевой системе, а какие - от нее.
При этом накладывается ограничение на взаимодействия, инициируемые целевой системой. В процессе таких взаимодействий данные должны передаваться только от целевой системы. Если это ограничение не выполняется, то необходимо разбить проблемные взаимодействия на меньшие составляющие.
В результате мы получим набор взаимодействий, инициируемых окружением целевой системы, и набор взаимодействий, инициируемых целевой системой. Взаимодействия первого типа имеют данные, передаваемые к целевой системе, мы будем называть их входными, и данные, передаваемые от целевой системы, мы будем называть их выходными. Взаимодействия второго типа содержат только данные, передаваемые от целевой системы, которые мы также будем называть выходными.
Каждому виду взаимодействий ставится в соответствие интерфейсная операция. Для взаимодействий первого типа интерфейсная операция имеет набор входных параметров, описывающих входные данные, и набор выходных параметров, описывающих выходные данные. Такие интерфейсные операции мы будем называть интерфейсными операциями-стимулами. Для взаимодействий второго типа интерфейсная операция имеет только выходные параметры, описывающие выходные данные. Интерфейсные операции такого типа мы будем называть интерфейсными операциями-реакциями.
Для описания требований к поведению целевой системы в рамках асинхронных взаимодействий используется спецификации соответствующих интерфейсных операций. Предусловие операции определяет, какие значения входных параметров являются допустимыми для передачи целевой системе, а постусловие операции определяет какие выходные значения параметров являются корректными для данных значений входных параметров.
Y =
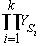
Мы будем считать, что каждый элемент дизъюнктивного объединения помечается именем интерфейсного операций и таким образом эти элементы не пересекаются между собой. множество отложенных реакций Z является дизъюнктивным объединением декартовых произведений множеств допустимых значений выходных параметров всех интерфейсных операций-реакций спецификации
Z =
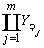
Мы будем считать, что каждый элемент дизъюнктивного объединения помечается именем интерфейсной операции и таким образом эти элементы не пересекаются между собой. множество переходов E состоит из всех переходов, удовлетворяющих обобщенным предусловию и постусловию спецификации
E = { ( v, ( x, y ), v' )







где предикаты preS =