Проверка сходимости для некоторых моделей

                Были проведены сопоставительные расчеты шарнирно опертой квадратной пластинки загруженной по всей площади равномерно распределенной нагрузкой. Расчеты выполнялись при четырех сетках конечных элементов — 4´4, 8´8, 16´16 и 24´24 (рис.20.1).

Рис.20.1. Изополя изгибающих моментов для расчетных схем

с различными сетками конечных элементов

                В таблице 20.2 приведены результаты по перемещениям, изгибающим моментам и поперечным силам для конечных элементов различного типа, полученные на упомянутых сетках, эти же данные проиллюстрированы на графиках, представленных на рис.20.2.

Таблица 20.2

		Перемещения центра плиты при сетке:
Тип КЭ		4x4		8x8		16x16		24x24
11/41		0,0180329		0,0172754		0,0170823		0,0170453
20/50		0,0166168		0,0169137		0,0169918		0,0170051
12/42		0,0161403		0,0168034		0,0169658		0,0169938
		Момент в центре плиты:
М -11/41		0,04781		0,04509		0,04443		0,04443
М -20/50		0,03991		0,04313		0,04393		0,04408
М -12/42		0,04787		0,04528		0,04432		0,04448
		Поперечная сила на краю:
Q -11/41		0,22		0,28		0,31		0,32
Q -20/50		0,37		0,4		0,43		0,44
Q -12/42		0,24		0,31		0,33		0,34

а)		б)
в)		Обозначения:                                 Рис.20.2. Сходимость результатов при равномерной нагрузке: а ? по прогибам, б ? по моментам, в ? по поперечным силам

Как видно из таблицы и рисунка, практическая сходимость имеет место для прогибов и изгибающих моментов при использовании конечных элементов всех типов, а для поперечных сил элементы 11-го типа дают значения, заметно отличающиеся от величин, полученных с использованием других конечных элементов. Отметим, что элемент типа 20/50 был использован в схеме, где он присоединялся только к четырем узлам, хотя имеется возможность ввести узлы на его сторонах (всего до восьми узлов). Контрольные расчеты при такой схеме использования показали, что точность результатов существенно возрастает и они приближаются к данным, получаемым на сетках вдвое большей густоты. Например, для сетки элементов 8х8 прогиб равнялся 0,01701, изгибающий момент ? 0,0442 и поперечная сила ? 0,278.

В другой серии численных экспериментов, когда та же пластинка была загружена сосредоточенной силой, результаты, представленные в таблице 20.3 и на рис.20.3, оказываются менее оптимистичными. Здесь замедляется скорость практической сходимости по моментам, и еще более существенно ? по поперечным силам, значения которых взяты в точке, расположенной на расстоянии четверти толщины от центра пластинки. По-видимому для поперечных сил вообще не следует брать во внимание значения для точек, столь близко расположенных около места приложения сосредоточенной нагрузки. Более детально этот вопрос анализируется ниже.

Таблица 20.3

		Перемещения центра плиты при сетке:
	Тип КЭ	4x4	8x8	16x16	24x24
	11/41	0.511522	0.494164	0.488470	0.487183
	20/50	0.466266	0.480460	0.484425	0.485222
	12/42	0.432918	0.470046	0.481375	0.483493
		Момент в центре плиты:
	М -11/41	2.61566	3.27276	3.93364	4.32066
	М -20/50	2.31761	3.04494	3.72290	4.11309
	М -12/42	1.89259	2.52465	3.17713	3.56252
		Поперечная сила около центра:
	Q -11/41	7.26	14.58	29.18	43.77
	Q -20/50	6.50	13.31	26.81	40.26
	Q -12/42	11.37	25.59	53.21	80.42
а)	б)
в)	Обозначения:                                 Рис.20.3. Сходимость результатов при нагружении сосредоточенной силой: а ? по прогибам, б ? по моментам, в ? по поперечным силам

                Следует отметить, что более быстрая сходимость результатов для некоторых типов конечных элементов дается за счет заметного увеличения времени счета. Поэтому следует сопоставлять потери времени от использования этих элементов с потерями на решение задачи на более густой сетке при использовании элементов другого типа.



20.1.4. Обход особых точек

Вблизи особых точек, таких, где имеется резкая концентрация напряжений, применение конечных элементов (равно как и других методов дискретизации) обычно затруднено, особенно в представлении поля напряжений. Приходится резко сгущать сетку конечных элементов и существенно увеличивать размер задачи.

Однако упомянутое сгущение сетки может и не привести к результату (см., например рис. 20.2.в), что подталкивает к дополнительному анализу ситуации. Одним из наиболее распространенных суждений является следующее ? сосредоточенная сила есть не существующая в природе абстракция и если бы она была создана, то, проткнув бы конструкцию любой прочности и не встречая сопротивления, унеслась бы в бесконечность. Выходит, что эта идеализация создает искусственную трудность, в борьбе с которой можно совершать героические подвиги, но практическая значимость таких подвигов весьма относительна. Следовало бы помнить о том, каким образом фактически реализована в конструкции та сила, которая идеализируется в форме сосредоточенной, тогда могут отпасть и вопросы о сходимости конечно-элементного решения к точному.

Мы рассмотрим указанную проблему на примере расчета плиты на упругом основании, к которой приложена сосредоточенная сила. Этот пример является часто используемой идеализацией при расчете фундаментных плит (сосредоточенной силой имитируется нагрузка, передаваемая колонной), аэродромных и дорожных покрытий (здесь сосредоточенная сила имитирует давление колеса) и в других практически важных случаях.

Проверка заданного армирования

Кроме подбора арматуры в постпроцессоре преду­смотрен также режим проверки заданного армирования. Для подготовки данных активизируется одноименный маркер на странице Характеристики групп. На странице Проверка заданного армирования (рис. 16.2.5) задается номер последнего проверяемого сечения элементов группы (естественно, подразумевается, что в группе заданы элементы, у которых совпадают жесткостные характеристики и количество сечений). Если проверяется каждое сечение, то заполняются соответственно столько строк в таблице, сколько задано сечений.

Если задана информация для проверки арматуры, то параметры заданной арматуры принимаются стартовыми при подборе.

В зависимости от модуля армирования в таблицу вводится следующая информация:

Для стержня 2D – значения AS1, AS2, AS3, AS4 задаются для несимметричного армирования в соответствии с

рис. 16.1.1а-г Для симметричного армированию значения АS1 = АS2, в позициях AS3 и AS4 задаются два числа, сумма которых равна АS3 (см. Рис. 16.1.1д-ж).

Для стержня 3D – значения AS1, AS2, AS3, AS4 задаются для несимметричного армирования в соответствии с

рис. 16.1.2а-г Для симметричного армированию значения АS1 = АS2, в позициях AS3 и AS4 задаются два числа, сумма которых равна АS3 (см. Рис.16.1.2д-ж).

Для плиты и оболочки в позициях AS1 – AS4 задаются проверяемые площади сечений продольной арматуры  AS1 (нижняя по X), AS2 (верхняя по X), AS3 (нижняя по Y), AS4 (верхняя по Y) в соответствии с рис.16.1.3.

Для балок-стенок в позициях AS1 и AS2 задаются два числа АS1 (по X) и АS2 (по Z) (см. Рис. 16.1.16). Размерность – квадратные сантиметры.

В позициях ASW1, ШАГ, ASW2, ШАГ  задаются величины проверяемых площадей сечений хомутов при определенном расстоянии между ними по длине элемента. ASW1 – шаг расстановки в плоскости  X1ОZ1 для стержней и плит; ASW2 –  шаг расстановки в плоскости X1ОY1 для стержней и в плоскости Y1ОZ1 – для плит. Размерность – квадратные сантиметры, сантиметры.

             Рис. 16.2.5. Страница

 Проверка заданного армирования

Проверка заданной арматуры

Если при проверке заданной арматуры указано несимметричное продольное армирование (AS1 не равно АS2), то результаты счета будут выводиться только в графах несимметричного армирования. В этом случае, если заданная величина площади сечения арматуры не увеличилась, то в графах симметричного армирования будут содержаться пробелы. В противном случае в этих графах ставится символ "**".

                Если для проверки задано симметричное продольное армирование (AS1=AS2), то результаты счета будут выводиться в графах симметричного армирования. В этом случае, если заданная величина площади сечения арматуры не увеличилась, то в графах несимметричного

армирования будут содержаться пробелы. В противном случае в этих графах ставится символ "**".

ЛИТЕРАТУРА

 

1.     Строительные нормы и правила. Бетонные и железобетонные конструкции. СНиП 2.03.01-84. M., Cтройиздат, 1985.

2.     Строительные нормы и правила. Строительство в сейсмических районах. СНиП II-7-81. M., Стройиздат, 1982.

3.     Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01 – 84). ЦНИИпромзданий Госстроя СССР, НИИЖБ Госстроя СССР. М.: Стройиздат, 1986.

4.     Карпенко Н.И. Теория деформирования железобетона с трещинами. М.: Стройиздат, 1976.

Расчет нагрузок от фрагмента схемы

Если мысленно отделить часть конструкции, то ее действие на оставшуюся часть сводится к некоторым нагрузкам. Постпроцессор расчета нагрузок от фрагмента схемы позволяет определить нагрузки в заданных узлах от отделенной части схемы, например, от наземной части расчетной схемы на фундаменты.

В качестве исходных данных для расчета служат группы узлов, в которых необходимо получить нагрузки, и группы элементов, приходящих в эти узлы. При расчете нагрузок на фундаменты задается также угол поворота участка фундамента вокруг оси Z, если оси инерции колонн не совпадают с осями фундамента под этими колоннами. Нагрузки могут быть вычислены как для каждого загружения, так и для комбинаций загружений.

15.1 Ввод исходных данных

Подготовку данных для расчета можно выполнить как при формировании расчетной схемы, так и в процессе графи­ческого анализа результатов. Выполняется это путем задания групп узлов и элементов в разделе инструментальной панели Группы. Дополнительная информация задается в разделе Специальные исходные данные Дерева проекта обращением к операции Нагрузки от фрагмента схемы.

Исходные данные можно задать двумя способами. Первый – предполагает задание элементов, от которых необходимо получить нагрузки (разрезаемые элементы) и явное задание узлов, в которых нагрузки будут получены. При втором способе отмечается весь изолируемый фрагмент. Нагрузки от него на остальную часть конструкции, включая реакции в связях, будут получены во всех узлах, лежащих на границе выделенного фрагмента. К числу узлов, лежащих на границе фрагмента, относятся узлы, примыкающие к части схемы, не вошедшей во фрагмент, а также узлы, в которых наложены связи.

При первом способе рекомендуется придерживаться такого порядка действий при подготовке исходных данных:

Ä        в разделе Группы активизировать функцию задания групп элементов –

;

Ä        отметить на схеме элементы (например, все или только элементы, примыкающие к узлам, в которых будут получены нагрузки);

Ä        сохранить группу элементов, задав ей имя – ;

Ä        активизировать функцию задания групп узлов – ;

Ä        отметить на схеме узлы, в которых необходимо получить нагрузки;

Ä        сохранить группу узлов, задав ей имя – ;

Ä        повторить две предыдущие операции для каждой группы узлов, принадлежащих другим участкам схемы.

Порядок действий при использовании второго способа повторяет первые три операции, описанные выше. Однако при сохранении группы элементов инициируется операция Создать сопряженную группу узлов, при выполнении которой группа узлов, лежащих на границе выделенного фрагмента, будет сформирована автоматически.

Расчет нагрузок может быть выполнен как в общем цикле решения задачи, так и самостоятельно в режиме постпроцессора. В первом случае исходные данные для расчета должны быть подготовлены до выполнения расчета. Во втором ? их можно подготовить и после завершения основного расчета.

 

Назначение групп узлов и элементов следует выполнять после упаковки данных.

 

15.2 Описание фрагментов

Для того чтобы выполнить расчет нагрузок от фрагмента схемы, следует задать дополнительную информацию, которая определяет режим выполнения расчета (по загруже­ни­ям и/или по комбинациям загружений), элементы, приходя­щие в узлы, в которых вычисляются нагрузки, а также сами узлы.

Дополнительная информация задается в разделе Специ­альные исходные данные Дерева проекта

обращением к операции Нагрузки от фрагмента схемы. После активизации этой операции появляется одноименное диалоговое окно (рис. 15.2.1). Рекомендуется следующий порядок работы в нем:

Ä      установить режим выполнения расчета – по загружениям и/или по комбинациям загружений;

Ä      выбрать в списке групп элементов группу, которая задана для выполнения расчета нагрузок от фрагмента схемы;



Ä      нажать кнопку [<<] и тем самым загрузить в окно Список элементов

номера элементов выбранной группы;

Ä      нажать кнопку Новый участок (здесь имеется в виду, например, часть фундамента, в узлах которого вычисляются нагрузки) ;

Ä      выбрать в списке Группы узлов имя группы, принадлежащей первому участку; нажать кнопку [<<] и тем самым загрузить список узлов выбранной группы в окно Список узлов;

Ä      ввести угол поворота участка фундамента, которо­му принадлежат узлы первой группы, вокруг оси Z общей системы координат (по умолчанию 0°).

                Если предусмотрен расчет нескольких участков фун­дамента с разными углами ориентации относи­тельно осей общей систе­мы координат, то необходимо нажать кнопку Новый участок и повто­рить все описан­ные выше действия с группа­ми узлов для нового участка, задав его угол ориентации, и т.д. Завершить ввод данных нажатием кнопки OK

диалогового окна.

Рис. 15.2.1.  Диалоговое окно

Нагрузки от фрагмента схемы

Набор узлов каждого участка можно откорректировать непосредственно в списке Группы узлов. Кроме того, преду­смотрена возможность удаления ошибочно заданных участков. Для этого необходимо установить номер удаляемого участка и на­жать кнопку

Удалить участок. Если необходимо исклю­чить расчет нагрузок от фрагмента схемы, следует нажать кнопку Удалить данные.



Не допускается наличие одинаковых номеров узлов в разных группах.

16. Армирование сечений железобетонных элементов

Постпроцессор предназначен для подбора арматуры в железобетонных элементах по предельным состояниям первой и второй групп в соответствии с требованиями СНиП 2.03.01-84. Бетонные и железобетонные конструкции.

                Расчет пpоизводится для железобетонных констpук­ций, выполняемых из тяжелого, мелкозеpнистого и легкого бетонов с пpименением аpматуpной стали классов А-I, A-II, A-III, A-IV, A-V, A-VI и аpматуpной пpоволоки класса Вр-I.



                Постпроцессор pаботает как в pежиме подбоpа арматуры железобетонного сечения, так и в pежиме проверки заданного армирования.

                Библиотека постпроцессора содеpжит четыре модуля армирования:

модуль 1 (Стержень 2D) – для армирования плоских стержневых железобетонных элементов прямоугольного, тавpового, двутавpового и кольцевого сечений по предельным состояниям первой и второй групп;

модуль 2 (Стержень 3D) – для армирования пpостpанственных стержневых железобетонных элементов прямоугольного, таврового, двутаврового сечений по пpедельному состоянию первой группы;

модуль 11 (Плита. Оболочка) – для армирования железобетонных оболочек по предельным состояниям первой и второй групп.

модуль 21 (Балка-стенка) – для армирования железобетонных балок-стенок по предельным состояниям первой и второй групп.

                Исходными данными для pаботы постпроцессора являются:

геометpия аpмиpуемого сечения;

pасчетные сочетания усилий;

информация о марке бетона, классе арматуры, расстояние до центра тяжести арматуры и т.п.

                Исходные данные задаются в диалоговом окне постпроцессора.

                Результатом работы постпроцессора являются площади "размазанной" арматуры. Результаты могут быть представлены в виде таблиц и графических материалов, выводиться на экpан или печать.

Ограничения реализации

При использовании постпроцессора следует учитывать некоторые ограничения реализации:

не реализован расчет сечений из ячеистого, поризованного и напрягающего бетонов;

не выполняется расчет предварительно напряженных железобетонных элементов;

не выполняется расчет элементов по предельному состоянию по деформациям и на выносливость;

набор сечений ограничен прямоугольником, тавром, двутавром и кольцевым сечением;

не контролируется предусмотренное СНиП 2.03.01-84 (п. 16.17) ограничение на диаметр арматуры при бетонах низких марок; максимальный диаметр арматуры задается пользователем;

не контролируется предельная ширина полок таврового и двутаврового сечений; расчетная ширина полок задается пользователем в соответствии с требованиями п. 3.16 СНиП 2.03.01-84;

не учитывается коэффициент gs5 для высокопрочной арматуры классов A-IV, A-V, A-VI, В-11, ВР-11, К7, К-19 при напряжениях выше условного предела текучести (табл. 24 СНиП 2.03.01-84);

при проверке по второму предельному состоянию расчет по закрытию трещин не производится.

 

 

 

 

 

 

 

 

 

16.1 Общие сведения о модулях армирования

Расчет по акселерограмме

                В перечисленных выше вариантах нагрузок было возможно точное вычисление yi(t). В остальных случаях решения yi(t) находим численно.

                В частности, при расчете на сейсмическую нагрузку по акселерограмме в каждый k-й момент времени

 задается вектор fk = f(tk). Тогда в (19.20) имеем Pi,k

= Pi(tk). Далее уравнения (19.19) решаются методом конечных разностей по схеме Ньюмарка. Получаем значения перемещений yi,k = yi(tk) и инерционных сил Si,k = Si(tk), по которым вычисляется экстремальное из числа рассмотренных моментов времени значение

                                                                Sj,o = maxk{ïwj yj(tk)ï}.                                                                                  (19.43)

Расчетная схема метода перемещений

                Поскольку в основу используемых алгоритмов положен метод перемещений, то идеализация конструкции должна быть выполнена в форме, приспособленной к использованию этого метода, а именно: система должна быть представлена в виде набора тел стандартного типа (стержней, пластин, оболочек и т.д.), называемых конечными элементами и присоединенных к узловым точкам.

                Тип конечного элемента определяется:

его геометрической формой;

набором узлов, которыми могут быть точки, как лежащие в вершинах геометрических фигур, так и на их сторонах, ребрах, поверхностях;

правилами, определяющими зависимость между перемещениями узлов конечного элемента и узлами системы – узлы элемента могут быть прикреплены к узлам системы жестко (полное совпадение всех перемещений) или с использованием шарниров и т.п. (см. ниже);

физическим законом, определяющим зависимость между внутренними усилиями и внутренними перемещениями, и набором параметров (жесткостей), входящих в описание этого закона;

выбором системы внутренних перемещений (деформаций) и соответствующих им внутренних усилий (напряжений), характеризующих напряженно-деформированное состояние элемента;

выбором аппроксимирующих (базисных, координатных) функций, с помощью которых перемещения произвольной точки конечного элемента однозначно определяются через перемещения его узлов;

набором допустимых нагрузок и воздействий, которые могут быть приложены непосредственно к конечному элементу, и способами их задания;

наличием или отсутствием правил дробления элемента на более мелкие части при детализации описания его напряженно-деформированного состояния или при уточнении мест приложения нагрузок и воздействий;

другими, более специфическими условиями (возможностью использования только в системах определенного типа, ограничениями на ориентацию по отношению к системе координат и др.).

                Узел в расчетной схеме метода перемещений представляется в виде абсолютно жесткого тела исчезающе малых размеров. Положение узла в пространстве при деформациях системы определяется координатами центра и направлениями трех осей, жестко связанных с узлом. Иными словами, узел мыслится как объект, обладающий шестью степенями свободы – тремя линейными смещениями, определяемыми как разности координат в деформированном и недеформированном состояниях, и тремя углами поворота. С узлами могут быть связаны и другие параметры, определяющие деформированное положение системы (дополнительные степени свободы).

                В методе перемещений элементы системы считаются присоединенными только к узлам расчетной схемы. Указанная особенность построения расчетной схемы не всегда подчеркивается в учебной и справочной литературе. Такой подход является приближенным, поскольку сосредотачивая эквивалентные усилия в узлах, условия равновесия конечных элементов некоторых типов (например, пластин и оболочек) можно выполнить только интегрально. На межэлементных границах нестержневых элементов мыслятся возможные разрезы, что заставляет обращать внимание на так называемое свойство совместности (конформности) элементов. Совместные элементы гарантируют совпадение перемещений и их необходимых производных для точек, расположенных на противоположных берегах разреза. Для несовместных элементов возникает необходимость выполнения дополнительных условий, компенсирующих возможные расхождения берегов разреза. Следует отметить, что все представленные в библиотеке комплекса элементы либо являются совместными, либо для них гарантируется выполнение дополнительных условий компенсации несовместности.

                Указанное выше условие примыкания элементов к узлам не всегда видно и при использовании традиционных способов изображения расчетной схемы. Так, расчетная схема, представленная на Рис.19.1,а в традиционной форме, может навести на мысль о непосредственном соединении элементов друг с другом, в то время как более детальное изображение по рис.19.1,б позволяет избежать такого умозаключения. Заметим также, что в детальном изображении видны и другие особенности реализации расчетной схемы, в частности, возможность выполнения одинаковых кинематических условий с использованием различных наборов связей (см. п.1.1.4).

                Предполагается, что вся расчетная схема состоит только из элементов заранее определенного типа. Список типов элементов, которыми оперирует расчетный комплекс, может видоизменяться и пополняться, однако каждой его конкретной версии соответствует вполне определенный набор типов элементов (библиотека конечных элементов), из которого могут быть выбраны части расчетной схемы.





Рис. 19.1

Наконец, следует сказать, что все узлы и элементы расчетной схемы нумеруются. Номера, присвоенные им, следует трактовать только как имена, которые позволяют делать необходимые ссылки. Например, можно указать узел, где приложена некоторая нагрузка, или перечислить узлы, к которым присоединен вполне конкретный элемент, или же составить список элементов, примыкающих к определенному узлу (это будет, так называемая “звезда элементов” в узле). Больше никаких других функций нумерация не выполняет и, в частности, она практически не влияет на время решения задачи из-за имеющейся в комплексе функции оптимизации профиля матрицы жесткости. Однако, выдача результатов расчета чаще всего производится в порядке нумерации узлов (перемещения) или элементов (внутренние усилия), поэтому говорить о полной независимости от нумерации все же не приходится.

Расчетные сочетания усилий (РСУ)

Вычисление РСУ производится на основании критериев, характерных для соответствующих типов конечных элементов – стержней, диафрагм, плит, оболочек, массивных тел. Для всех типов элементов РСУ выбираются по критерию наибольших напряжений, рассматриваются отдельные критерии, учитывающие, например, особенности работы железобетона. Так для стержней, находятся сочетания с максимальной растягивающей и сжимающей продольной силой.

                При расчете учитываются требования нормативных документов и логические связи между загружениями, накладываемые нормативными документами или существом решаемой задачи.

Введено понятие взаимоисключающих загружений, то- есть таких, которые в одно сочетание одновременно входить не могут. Так, например, активное ветровое воздействие на сооружение одновременно с двух (трех, четырех) сторон учитывать не следует. Все эти ветровые воздействия можно включить в одну группу взаимоисключающих загружений.

Понятие сопутствующих загружений введено для того, чтобы загружение сопутствующее, то есть порожденное основным, не включалось бы в РСУ без основного. Так, например, усилия от торможения тележки крана не могут включаться в РСУ, если туда не вошли усилия от давления колес крана. Нагрузка же от крана может действовать и без сочетания с тормозной. Имеется возможность ограничить и число одновременно учитываемых в РСУ воздействий от крановых и тормозных нагрузок, что вытекает из требования соответствующих норм.

Понятие объединенно-кратковременных нагрузок введено для того, чтобы дать возможность включать в основное сочетание не одну из кратковременных нагрузок, а их группу (либо наиболее опасную по прочности комбинацию нагрузок из этой группы). При назначении коэффициентов сочетания, зависящего от числа действующих нагрузок, эта группа засчитывается как одна временная нагрузка от одного источника или как нагрузка от нескольких источников, совместное действие которых учтено при определении значения нагрузок (например, гололедно-ветровая нагрузка).

Нормами проектирования предусмотрено, что некоторые виды нагрузок в некоторых сочетаниях не должны учитываться полностью. Поэтому произведена классификация по видам загружений (постоянная, временная, крановая и т.д.) и предоставлена возможность задавать коэффициенты, с которыми данное загружение может входить в основное и другие сочетания.

Расчетные сочетания усилий могут быть вычислены как в общем потоке расчета задачи, так и отдельно, после завершения расчета на статические и динамические воздействия. В первом случае исходные данные готовятся после завершения формирования расчетной схемы и ввода загружений, во втором – данные могут быть введены после завершения расчета по загружениям.

Подготовка исходных данных для вычисления РСУ выполняется только после задания всех загружений. Функция подготовки вызывается из Дерева проекта в разделе Специальные исходные данные, подраздел Расчетные сочетания усилий.



   Рис. 11.1. Диалоговое окно

Расчетные сочетания усилий

В диалоговом окне Расчетные сочетания усилий (рис.11.1) автоматически записы­ваются имена всех сформированных загружений. Каждому загружению выделена одна строка таблицы, которая включает номер загружения, его имя, список для установки типа загружения и столбцы со специальной информацией, характе­ризующей загружение и его взамосвязь с другими загружениями. В связи с ограничением места в диалоговом окне таблица состоит из двух блоков – нижнего и верхнего, связанных общей линейкой прокрутки. При помощи этой линейки выполняется листание по строкам. По этой же причине в нижнем блоке таблицы количество видимых столб­цов с коэффициентами РСУ ограничено тремя. Для доступа к остальным столбцам с коэффициентами использу­ются кнопки [<<], [>>].

Порядок выполнения операций при подготовке данных для расчета РСУ:

Ä        используя списки типов загружений, установ­ленные в каждой строке, назначить всем загружениям их тип; по мере назначения типа в таблицу автома­тически заносятся коэффициенты РСУ, принятые по умолчанию;



Ä        заполнить последовательно для каждого загруже­ния столбцы с параметрами;

Ä        заменить в случае необходимости значения коэф­ фициентов на требуемые по условиям решения задачи;

Ä        нажать кнопку Список элементов и назначить элементы или группы, для которых выполняется расчет (по умолчанию расчет выполняется для всех элементов расчетной схемы);

Ä        если предполагается выполнение унификации и/или создание групп унификации, то вызвать одноименные  диалоговые окна, нажав соответ­ственно кнопки Унификация и Группы.

Если при подготовке данных на входном языке (текстовое описание) была задана информация для вычисления РСУ, то после вызова диалогового окна она будет автома­тически введена в таблицу и может быть при необходимости откорректирована. Порядок выполнения корректировки тот же, что и при задании данных.

Если в столбце Объединение кратковременных загружений (к ним относятся загружения, помеченные как временное длительно действующее, кратковременное

и кратковременное, длительность действия которого мала) группа загружений помечена одинаковой цифрой, то она при определенных условиях может попасть в первое основное сочетание в любой комбинации сумм этих загружений.

В столбце Знакопеременные единицей помечаются знакопеременные загружения. (практически всегда должны быть объявлены знакопеременными динамические загружения, а также тормозные нагрузки кранов).

В первом столбце Взаимоисключающие каждому загружению из группы взаимоисключающих загружений присваивается номер от 1 до 9 (т.е. может быть создано до 9 групп таких загружений). Второй столбец пока не исполь­зуется.

В столбцах Сопутствующие

указываются номера сопутствующих загружений, т.е. таких, действие которых обусловлено наличием данного загружения. К таким загружениям, например, относятся тормозные, которые попадут в РСУ только совместно с крановыми и в строке кранового нагружения указаны как сопутствующие ему.



 

Рис. 11.2. Диалоговое окно

      Список элементов

На информацию о взаимодействии загружений накла­ды­ва­ются логические ограничения, приведенные в табл.11.1:

объединение кратковременных нагрузок допускается лишь для кратковре­менной и кратковре­менной с малой длитель­ностью действия нагрузок;

не все виды нагрузок могут быть объявлены сопутствую­щими

тормозная нагрузка может сопутствовать только крановой;

двойное сопутствие не допускается;

любая сопутствующая нагрузка не может попадать в группы объединения и взаимоисключения.

Таблица 11.1

Вид нагружения	Объеди­нение 2 и 7	Зна­копере­мен­ность	Взаимоис-ключение	Сопутствие
0 - постоянное	-	-	-	-
1 - временное дли­тельно действу­ющее	+	+	+ 1	+ 1, 2, 5, 6, 7
2 - кратковре­менное	+	+	+ 2, 5, 6, 7, 9	+ 2, 5, 6, 7, 9
3 - крановое	-	-	+3	+4
4 - тормозное	-	+	-	-
5 - сейсмическое	-	+	+ 2, 5, 6, 7	+ 2, 5, 6, 7
6 - особое (кроме сейсмического)	-	+	+ 2, 5, 6, 7, 9	+ 2, 5, 6, 7, 9
7 - кратковре­менное, длитель­ность действия которого мала	+	+	+ 2, 5, 6, 7	+ 2, 5, 6, 7
9 - статическое ветровое при учете пульсации ветра	-	-	-	-
В таблице использованы следующие обозначения: "-" (минус) не допускается; "+" (плюс) - допускается, цифры после плюса - виды загружений, которые допускается объявлять сопутствующими либо взаимоисключающими.

В столбце Коэффициент надежности вводится коэффициент надежности по нагрузке gf. Формируемые по умолчанию коэффициенты имеют следующие значения:

для постоянных загружений gf = 1.1;

для временного загружения gf = 1.2;

для особых воздействий gf = 1.0;

для кратковременных с малой длительностью gf = 1.4.

Следует отметить, что коэффициент надежности используется только модулем подбора арматуры для перехода от расчетных значений нагрузок к нормативным.



В столбце Доля длительности

указывается, какая часть нагрузки Кg ( в долях от единицы) принимается в данном загру­жении как длительно действующая. По умолчанию принима­ются следующие значения Кg:

для постоянных и длительно действующих загружений Кg = 1;

для крановых Кg = 0.6;

для прочих Кg = 0.0.

Столбцы Коэффициенты РСУ

используются для записи коэффициентов, с которыми усилия от каждого загру­жения входят в РСУ.  Столбец 1-е главное (1) предназначен для формирования 1-го основного сочетания нагрузок, в котором учитываются усилия от всех постоянных, длительно действующих и только от одного наиболее опасного временного загружения или (при наличии номера в столбце Объединение кратковременных) от группы объединенных временных загружений. В столбец 2-е главное (2) заносятся коэффициенты для формирования  РСУ по 2-му сочетанию нагрузок, а в столбец Особое (3) – по особому.

Если эти столбцы не заполнены, то в них коэффи­циенты формируются по умолчанию следующим образом:

столбец (1) – первое основное сочетание: для всех видов загружений, кроме особых, К1=1 (для особых К1=0);

столбец (2) – второе основное сочетание: для постоянных К2=1; длительно действующих К2=0.95; для кратковременных, крановых и тормозных К2=0.9; для особых К2=0;

столбец (3)– особое сочетание: для постоянных К3=0.9; для длительно действующих К3=0.8; для кратковременных К3=0.5; для крановых и тормозных К3=0; для сейсмических К3=1; для прочих динамических К3=0.

                Блок РСУ выполнен для работы с заданными в загружениях расчетными  нагрузками. Использование норма­тив­ных нагрузок не предусмотрено.

В практике возможны случаи, когда для разных элементов схемы требуется применить разные коэффициенты сочетаний в одном и том же загружении. Такие элементы объединяются в группы (не путать с группами элементов, создаваемыми при формировании расчетной схемы и анализе результатов). Групп может быть две. Они формируются в диалоговом окне Группы, которое вызывается после нажатия одноименной кнопки в окне Расчетные сочетания усилий. Один и тот же элемент может входить в обе группы. Для этих групп в таблице формируют дополнительные столбцы (с 4-го по 15-й) коэффициентов РСУ.

В тех случая, когда расчетные сочетания усилий необходимо вычислить не для всех элементов схемы, воспользуемся кнопкой Задание списка элементов, после нажатия на которую появляется диалоговое окно Список элементов (рис. 11.2.). Элементы могут быть введены с использованием групп. При этом доступны как группы, заданные для подбора арматуры, так и другие группы элементов. Если список вводится без использования групп, он готовится по следующим правилам:

номера элементов вводятся через пробел;

в случае подряд пронумерованных элементов первый и последний элементы ряда пишутся через дефис (например: 1-23 34 45 76 87-125).

Список, полученный путем ввода групп, может быть откорректирован.

 Раздел Справка содержит пункты

Инструментальная панель

Размещается под меню и содержит разделы с элементами управления, набор которых зависит от установленного режима. Переключение страниц  выполняется указанием курсора на “закладки" с наименованием разделов. Функции и режимы инструмен­тальных панелей пре- и постпроцессора описаны в соответ­ствующих разделах.

Диалоговые окна

В тех случаях, когда для выполнения операции требуются дополнительные данные или установки, на экран выводится соответствующее диалоговое окно. Диалоговые окна включают различные элементы управления – таблицы, кнопки, поля ввода, списки и т.п. Ввод, удаление или изменение данных выполняется с клавиатуры. Если выход из диалогового окна выполняется нажатием кнопки ОК, то все выбранные установки запоминаются. Если для выхода использована кнопка Cancel  (Отмена), то новые установки не сохраняются и при работе будут использоваться выбранные ранее или принимаемые по умолчанию.

Фильтры

            Служат для управления отображением расчетной схемы. С помощью фильтров отбираются и фиксируются некоторые однотипные объекты расчетной схемы, с которыми предполагается организовать работу (например, с помощью фильтра можно из всех стержней отобрать только верти­кальные), назначаются вид и правила отображения характери­стик и атрибутов расчетной схемы, а также узлов и элементов. Для более детальной настройки фильтров используются диалоговые окна, которые вызываются указанием курсора на панель фильтров после нажатия правой кнопки мыши.

Панель Фильтры отображения

оформлена в виде специального окна, которое содержит набор кнопок для выбора параметров отображения и устанавливается (или закрывается)  кнопкой 

,  размещенной в разделе Управление

инстру­мен­­тальной панели. Это окно может иметь любые размеры и находиться в любой части экрана.

                Кроме фильтров управления отображением, есть фильтры управления выбором узлов и элементов. Эти фильтры доступны в диалоговом окне Выбор узлов и элементов.

                Более подробно работа с инструментальными панелями и фильтрами рассматривается в разделе 8.2.

Пиктограммы

            В инструментальных панелях для инициализации операций используются кнопки с пиктограммами (или как их называют в Windows – иконами). Ограниченное пространство кнопки не всегда позволяет сделать пиктограмму адекватной смыслу операции, которую она символизирует. Для облегчения освоения комплекса и упрощения работы с ним используются различные средства. Во-первых, это информационная строка, в которую в момент попадания курсора в поле кнопки выводится краткое описание соответствующей кнопке операции. Во-вторых, это приведенная ниже система символических изображений в пиктограммах, которая отражает суть операции и является общей для всего комплекса.

  –  ОК  – выполнить операцию

  –  отказ от выполнения уста­новленной опера­ции

  –  восстановить исходный вид схемы

  –  запомнить загружение

  –  функции работы с элемента­ми

 – буква “R” –  жесткостные характеристики

  –  функции работы с узлами

  –  знак “плюс” – добавление узлов или элементов

  –  стрелка влево – возврат удален­ных узлов или элементов

  – знак “минус”  –  удаление узлов или элементов

 –  знак “деление” – дробле­ние эле­ментов

  –  буква “С” –  создание схемы или контура

  – “вопросительный знак” – отображение  или получение ин­формации

Если в правом нижнем углу пиктограммы изображена черная стрелка, направленная вправо, например , то это означает, что при нажатии на кнопку будет раскрыта группа кнопок управления соответствующим режимом.

Рекомендации по настройке среды Windows

Для того чтобы при работе с комплексом SCAD не возникало лишних проблем, желательно настроить среду Windows. Наилучшие результаты дает стандартная цветовая гамма, предлагаемая разработчиками Windows. Если пользователь все же решил сменить цвета, то не рекомендуется выбирать очень яркие. На их фоне могут плохо читаться элементы управления, особенно пиктограммы в  кнопках.



Обязательно обратите внимание на настройку монитора. Рекомендуется использовать мониторы с экраном не менее 15”. Для них оптимальной является разрешающая способность 1024*768 точек, хотя можно работать и в режиме 800*600. Для мониторов больших размеров можно исполь­зовать и более высокую разрешающую способность. В любом случае, “решающее слово” за техническими возможностями дисплея и установленной в машине видеокартой.

Выбор цветовой шкалы также определяется характеристиками видеокарты. Для получения качественного изображения не рекомендуется устанавливать менее 256 цветов. При анализе изополей изображение очень высокого качества можно получить при цветовой шкале с большим количеством цветов.

При выборе шрифта следует помнить, что от размера шрифта зависят размеры диалоговых окон. При установленном разрешении экрана 800*600 точек настройка монитора на крупный шрифт может привести к тому, что некоторые окна не будут целиком помещаться на экране. В то же время при разрешении 1600*1240 мелкий шрифт будет трудно читаемым.

Кроме стандартных средств настройки среды в комп­лексе SCAD реализованы и внутренние функции настро­йки. Их описание приводится ниже.

Загрузка комплекса

Включаем компьютер и шаг за шагом начинаем выполнять описанные ниже действия. Уже через час вы почувствуете, что умеете или, по крайней мере, понимаете, как работать с комплексом SCAD для Windows.

Для того чтобы начать работу с комплексом, необходимо установить курсор на пиктограмму SCAD и дважды нажать левую

кнопку мыши. На фоне окна инициализации появится изображение заставки (рис.1.2). Загрузка комплекса продолжается несколько секунд. В течение этого времени на экране установлен курсор “ожидания”  в виде песочных часов (если, конечно, на вашем компьютере он не заменен на более экзотический). Об окончании загрузки сигнализирует смена курсора ожидания на рабочий курсор – стрелку.

Рис. 1.2. Окно инициализации Structure CAD



Окно инициализации содержит меню и инструмен­тальную панель с кнопками управления. Меню состоит из трех разделов – Проект, Опции и Справка, описанных выше.

Инструментальная панель окна инициализации содер­жит пять кнопок. Четыре первые кнопки дублируют аналогич­ные функции раздела меню Проект, позволяя выполнить соответствующие операции более коротким путем.

В тех случаях, когда действие, вызываемое нажатием кнопки, недоступно (например, сохранение проекта до того, как он был создан или открыт) – пиктограмма кнопки отобра­жается в светло–серых тонах (серая кнопка).

 ? завершение работы

 ? создание нового проекта

 ? открытие ранее созданного проекта

 ? сохранение проекта

 ? полноэкранный режим работы



“Серые” кнопки будут появляться всякий раз, когда какой-либо режим, функция или операция не могут быть выполнены.

1.1 Создание нового проекта



Для создания нового проекта установите курсор на одноименную кнопку  раздела Управление

инструментальной панели и нажмите левую кнопку мыши. На экране появляется диалоговое окно Новый проект (рис. 1.1.1), в котором задается информация о проекте: наименование, объект, заказчик и т.п., а также назначается тип расчетной схемы. Диалоговое окно Новый проект, как и большинство других диалоговых окон, имеет три командные кнопки: OK, Отмена и Справка.



Рис. 1.1.1. Диалоговое окно

        ,Новый проект

OK – нажимается после завершения работы с диалоговым окном и закрывает его с автоматическим сохране­нием всей введенной информации.

Отмена – выполняется выход из окна без сохранения введенной информации.

Справка – обращение к справочной информации.

Кнопка Единицы измерения используется в тех случаях, когда единицы измерения,  которые предполагается использовать при подготовке данных и выполнении расчета, отличаются от установленных по умолчанию.

Обратите внимание на возможность выбора Типа схемы из списка, приведенного на рис. 1.1.2. Тип схемы определяет состав и максимальное количество степеней свободы в узлах расчетной схемы и характеризует особенности ее напряженно–деформированного состояния. Назначаемый тип схемы должен включать все необходимые степени свободы для используемых в схеме конечных элементов. По умолчанию устанавливается тип 5 – система общего вида.





Рис. 1.1.2. Список выбора типа схемы

В правой части окна Новый проект расположены кнопки для выбора норм проектирования железобетонных и металлических конструкций.

При нажатии кнопки ОК в

диалоговом окне Новый проект на экран выводится стандартное окно Сохранение проекта. В этом окне задается имя файла, которое будет присвоено файлу проекта, всем служебным файлам и файлам с результатами, порождаемым в процессе работы комплекса.

После небольшой паузы, связанной с регистрацией нового проекта в системе, управление передается  Дереву проекта (рис. 1.1.3), которое содержит четыре раздела первого уровня, фактически – этапы решения задачи: Исходные данные, Расчет, Результаты и

Конструирование. Эти разделы содер­жат ссылки на разделы второго уровня, которые детализируют выполняемые операции, например, Расчетная схема, Линейный расчет или Печать таблиц. Разделы Расчетная схема и Специаль­ные исходные данные включают подразделы с  перечнем исходных данных.



Рис. 1.1.3. Дерево проекта

Дерево проекта отобра­жает состояние проекта, т.е. наличие или отсутствие в проекте соответствующего вида данных, а также доступность функций, например, расчета или анализа данных. Из Дерева проекта можно инициализировать любую функцию – ввод данных, расчет или графический анализ результатов. Для этого доста­точно установить курсор на наименование

соответству­ющей ветви Дерева проекта и нажать левую кнопку мыши. Кроме того, Дерево проекта иллюстрирует структуру комплекса.

 

Раздел Управление инструментальной панели препроцессора

Работу по созданию нового проекта начнем с формирования расчетной схемы. Для этого установим курсор на раздел Расчетная схема Дерева и нажмем левую кнопку мыши. Управление будет передано графическому препроцес­сору, с помощью функций которого и выполняется синтез расчетной схемы. Инструментальная панель препроцессора содержит различные функции создания геометрии схемы, назначения граничных условий, нагрузок и др. После старта препро­цес­сора в инструментальной панели активен раздел Управление



инструментальной панели препроцессора (рис. 1.1.4).

Рис. 1.1.4. Раздел Управление инструментальной панели препроцессора

В этом разделе расположены четыре кнопки, дубли­ру­ющие одноименные операции меню Проект, а также допол­ни­тельные кнопки:

 Печать

– обеспечивает вывод на принтер установленного на экране изображения схемы;

 Выход в Дерево проекта – после нажатия на эту кнопку пре­­про­­цессор закрывается и управление передается Дереву проекта;

 Исключение из проекта удаленных узлов и элементов ? используется в тех случаях, когда  работа по созда­нию схемы закончена и нет необходимости сохранять инфор­ма­цию об удаленных узлах и элементах. После активи­зации этой функции все удаленные объекты из схемы исклю­ча­ются, а остав­шиеся получают новые номера (Упаковка данных).

 Показать/скрыть фильтры – с помощью этой кнопки мож­­но убрать или вернуть на экран панель с фильтрами.

 Показать/скрыть панель управления визуализацией – с помощью этой кнопки панель можно убрать с экрана или вернуть на экран.

 Сохранение образа экрана – после активизации этой функции сохраненяется текущее отображение схемы в формате Windows метафайла (файл с расширением WMF). Полученное изображение можно поместить в отчет с результатами расчета.

 Сохранение фрагмента схемы – позволяет сохранить видимый на экране фрагмент расчетной схемы в виде самостоятельного проекта.

1.2 Синтез схемы, расчет и анализ результатов

Приводится “экспресс-описание” функций форми­ро­ва­ния расчетной схемы, выполнение расчета и анализ результатов. Выполнив шаг за шагом описанные ниже действия, мы создадим простейшую схему, не вдаваясь в подробности, связанные с ее модификацией, и используя при этом только стандартные возможности комплекса. Наша цель – освоить принципы управления.

                Операции синтеза расчетной схемы и анализа резуль­татов расчета реализованы в единой графической среде. Расположение элементов управления и собственно управле­ние комплексом в окнах этих режимов одинаково. Отличается только набор функций.



 

Ввод параметров расчетной схемы

Установим курсор на закладке Схема и нажмем левую кнопку мыши.  В поле инструментальной панели находятся кнопки создания различного вида расчетных схем. Нажмем на первую из них – Генерация прототипа

рамы.

  кнопка Генерация прототипа рамы.

                На экран выводится диалоговое окно выбора конфигурации рамы (рис.1.2.1).

Рис.1.2.1. Диалоговое окно

Выбор конфигурации рамы

Для назначения прототипа рамы достаточно указать курсором на пиктограмму с изображением прототипа (или на кнопку справа от него) и нажать левую кнопку мыши.

В начальном состоянии активна кнопка выбора много­этаж­ной многопролетной рамы. Подтвердим выбор нажатием кнопки ОК.

В появившемся диалоговом окне Задание параметров регулярной рамы (рис. 1.2.2) выполняется ввод геометрических размеров рамы, назначаются жесткости элементов и наклады­ваются связи в узлах. Для ввода размеров используются две таб­лицы:  левая – для описания пролетов и правая  – для описания этажей.

Рис.1.2.2. Диалоговое окно

Задание параметров регулярной рамы

В качестве учебной схемы используем пример, приведенный на рис. 1.2.3. Введем в таблицу описания пролетов три пролета по 6 м, а в таблицу описания этажей – двенадцать этажей по 4 м и один этаж высотой 2.8 м (рис.1.2.3).

После ввода геометрических параметров рамы можно задать связи в узлах (закрепить схему), описать жесткостные характеристики элементов, а также установить тип конечных элементов. Для задания связей воспользуемся набором кнопок, установленных в правой части диалогового окна. Активизируем кнопки X, Z и Uz, что означает назначение связей по соответствующим направлениям. Для ввода жесткостных харак­те­ристик колонн и ригелей служат кнопки Колонны и Ригели, а для назначения типов элементов –  кнопка Назначение типа КЭ.



Рис. 1.2.3. Расчетная схема

 

Работа с таблицами

Для ввода табличной информации в диалоговых окнах используются универсальные таблицы. При вводе числовых данных в таблицы необходимо соблюдать следующие правила:

разделителем дробной и целой частей числа является точка;



при вводе чисел с плавающей запятой можно пользоваться экспо­ненциальной формой представления, например, 3е-5;

после завершения ввода числа следует нажать клавишу Enter, после чего поле ввода перейдет к следующей ячейке таблицы;

в тех случаях, когда в диалоговом окне для ввода используются две таблицы (рис. 1.2.2), переход к следующей таблице осуществляется нажатием клавиши табуляции – Tab;

введенную в таблицу информацию можно сохранить в сис­тем­ном буфере (clipboard), для этого следует выделить стро­ки с сохраняемой информацией и нажать клавиши Ctrl+Ins;

информация в таблицу может быть перенесена из систем­ного буфера, для этого нужно выделить строки, в которые вводится информация, и нажать клавиши Shift+Ins;

для удаления или очистки нескольких строк (блока) или вставки новой строки следует:

Ä      установить курсор на номер первой строки блока, нажать левую кнопку мыши и, не отпуская, протянуть до нужной строки (строки блока будут отмечены);

Ä      нажать правую кнопку мыши (курсор при этом должен находиться в поле таблицы) и вызвать меню;

Ä      выбрать в меню необходимую операцию (Удалить блок, Очистить блок, Вставить строку);

Ввод жесткостных характеристик элементов

При задании параметров рамы предполагается, что введенные значения жесткостных характеристик колонн назначаются всем колоннам. Аналогично назначаются жесткости всем ригелям. Для ввода жесткостных характеристик колонн нажмем на кнопку Колонны и выполним операции назначения в появившемся много­страничном диалоговом окне Жесткости стержневых элементов (рис. 1.2.4).

       Рис. 1.2.4. Диалоговое окно

Жесткости стержневых элементов

                На первой странице этого окна (Выбор типа жесткости) следует активизировать опцию Параметрические сечения, т.е. жест­костные характеристики элементов будут вычисляться автома­тически в зависимости от формы и размеров заданного сечения. После этого укажем на закладку Параметрические сечения и зададим характеристики сечения колонн (рис. 1.2.5).





Рис. 1.2.5. Страница

Параметрические сечения

Порядок работы следующий:

Ä    из списка Материал выбрать марку бетона, например, В15;

Ä    нажать на кнопку с изображением сечения колонны, в данном случае – прямоугольник;

Ä    ввести размеры сечения в полях ввода;

Ä    для контроля введенных данных нажать кнопку Контроль;

Ä    если назначения корректны – нажать кнопку ОК (окно закрывается);

                После выполнения последней операции управление вновь перейдет к диалоговому окну задания параметров рамы (рис. 1.2.2). Нажмем кнопку Ригели и выполним описанные выше действия для назначения жесткостных характеристик ригелей. Обратите внимание на рис. 1.2.3 – ригели в отличие от колонн имеют тавровое сечение.

Назначение типов конечных элементов

При генерации рамы для всех элементов автоматически устанавливается тип элемента, соот­ветствующий Типу схемы, назначенному при создании проекта. Для смены типа элемента нажмем кнопку Назначение типов конечных элементов и в появившемся диалоговом окне (рис. 1.2.6) выберем необхо­димый тип. В нашем случае – тип 2 (стержень плоской рамы).



Рис. 1.2.6. Диалоговое окно

Назначение типа элемента

При назначении типа элемента обратите внимание на информацию, помещаемую слева от пиктограммы с изображе­нием элемента.

После установки типа элемента нажмем кнопку ОК и вернемся в диалоговое окно Задание параметров регулярной рамы.

Генерация схемы

Так как все параметры рамы определены, то после нажатия кнопки ОК выполняется генерация расчетной схемы. Здесь следует отметить, что процесс генерации, т.е. запись всех данных о расчетной схеме в память, может занимать некоторое время (2-3 с) и нам следует подождать, пока созданная нами схема не появится на экране (рис.1.2.7).

 

Рис. 1.2.7. Расчетная схема рамы

После того, как схема создана, можно воспользоваться фильтрами управления отображением (см. рис. 1.1) и получить информацию о номерах узлов и элементов, типах жесткости и типах элементов. Для этого следует активизировать соответ­ствующие кнопки на панели фильтров, показанные ниже.



 – номера элементов

 – типы элементов

 – связи

 – номера узлов

 – типы жесткости

 – отображение узлов

Если нажать все кнопки одновременно, информации на схеме может оказаться слишком много для зрительного анализа. Удобнее выводить информацию одного вида. При нажатии кнопки фильтров (она как бы “утапливается”) соответствующая ей информация выводится на экран. При повторном нажатии кнопка “отжимается” и информация скрывается.

На рис. 1.2.7 приведена полученная расчетная схема с отображением на ней меток узлов, их номеров и мест установки связей.

В результате проделанной работы сформирована расчетная схема, заданы связи в узлах, назначены типы конечных элементов и их жесткостные характеристики. Для того чтобы выполнить расчет, осталось задать нагрузки.

 

Выбор элементов

Операции назначения каких-либо параметров узлам или элементам (в данном случае – значений нагрузки) выполняются только для выбранных объектов. Выбрать – это значит указать курсором на объект и нажать левую кнопку мыши, после чего объект маркируется (отмечается) красным цветом.

По умолчанию активным является курсор для выбора одного узла или элемента – перекрестье с мишенью. Для указа­ния элементов, к которым прикладывается нагрузка, можно воспользоваться им. Но в этом случае следует последо­вательно выбирать каждый элемент. Если параметры назнача­ются одновременно нескольким элементам, то удобнее воспользоваться одним из курсоров с рамкой – прямоугольной или полигональной. Переключение на курсор другого вида выполняется с помощью кнопок, расположенных в нижнем левом углу окна, или в диалоговом окне Выбор узлов и элементов (рис. 1.2.8).

Это окно открывается нажатием правой кнопки мыши в рабочем поле. Кроме назначения вида курсора в этом окне можно установить и правила выбора элементов в зависимости от их положения в схеме (фильтры выбора).



Рис. 1.2.8. Диалоговое окно

Выбор узлов и элементов

                Порядок действий следующий:

Ä      нажать правую кнопку мыши при положении курсора в рабочем поле;



Ä      с помощью кнопок группы Выбор стержней назначить ориентацию выбираемых стержневых элементов (например, расположенных вертикально);

Ä      нажать кнопку с изображением курсора – прямоугольной рамки.

                В результате окно закроется и на экране появится выбранный курсор. Так как была нажата кнопка Вертикальные элементы, то при охвате рамкой всей схемы выбраны будут только колонны. При активной кнопке Горизонтальные элементы выбираются только ригели. При использовании курсоров-рамок выбираются только те элементы, все узлы которых попали в рамку.

При повторном указании на выбранный объект выбор отменяется.

Задание нагрузок

Функции задания нагрузок содержатся в разделе Загружения

инструмен­тальной панели (рис. 1.2.9).



Рис. 1.2.9. Раздел Загружения

инструментальной панели препроцессора

Режим задания нагрузок включает функции, обеспечивающие автоматическое формирование собственного веса конструкции, задание динамических и статических нагрузок различного вида на узлы и элементы схемы, сохранение назначенных нагрузок в виде схем загружений или групп нагрузок.

Зададим нагрузки на учебную расчетную схему в виде двух загружений:

Загружение 1 – описывает постоянную нагрузку на перекрытиях и покрытиях и собственный вес колонн, которые задаются как равномерно распределенная нагрузка на ригели – 4.36 т/м, и равномерно распределенная нагрузка на колонны – 0.66 т/м. Нагрузки задаются по направлению оси Z общей системы координат;

Загружение 2 – описывает временную с пониженным нормативным значением нагрузку. Задается аналогично загружению 1, но с другими значениями нагрузок – соответственно 3.57 и 0.54 т/м.

Для задания этих нагрузок воспользуемся следующими кнопками инструментальной панели:

  ввод нагрузок на стержневые элементы;

  очистка текущего загружения или группы;



  запись загружения.

Для ввода нагрузок необходимо выполнить следующие операции:

Ä    нажать кнопку задания нагрузок на стержневые элементы  и задать в открывшемся диалоговом окне (рис. 1.2.10) вид, направление и значение первой нагрузки;

Ä    нажать кнопку ОК в диалоговом окне;

Ä    выбрать на схеме элементы, которым назначается нагрузка;

Ä    нажать кнопку  в инструментальной панели режима Загружения;

Ä    повторить описанные выше действия для второго вида нагрузки первого загружения.

Рис. 1.2.10. Диалоговое окно

Задание местных нагрузок на стержневые элементы

               

Если активизировать фильтр отображения распреде­лен­ных нагрузок , то введенные нагрузки будут показаны на расчетной схеме. При включенном фильтре визуализации значений нагрузки  рядом с нагрузкой будет показано ее значение.

Фрагмент расчетной схемы с отображением заданных нагрузок показан на рис. 1.2.11.

Рис. 1.2.11. Отображение нагрузок на фрагменте расчетной схемы

                Для записи загружения надо нажать кнопку  в инструментальной панели. В диалоговом окне Сохранить загружение ввести имя загружения и нажать кнопку ОК. Ввод имени не является обязательным, но эта информация позволяет лучше ориентироваться при анализе исходных данных и результатов расчета. Номер загружению будет присваивается автоматически (с согласия пользователя), о чем сообщается в специальном окне.

Перед тем, как ввести следующее загружение, восполь­зуйтесь операцией  – очистка текущего загружения. При ее выполнении происходит очистка схемы от нагрузок текущего загружения. После этого можно готовить новое загружение. Если при записи загружения ему присвоить номер ранее созданного, то оно будет записано вместо него.

Для завершения ввода текущего загружения его необходимо сохранить  (записать в проект).

В противном случае загружение не будет учтено при выполнении расчета.



 

 

 

 

 

 

 

 

 

 

 

Математика подобно жернову перемалывает

  лишь то, что под него засыпают

Т. Г. Гексли

Расчет

Введенных данных достаточно, чтобы выполнить расчет учебной схемы. Для этого нам необходимо вернуться в Дерево проекта. Активизируем закладку Управление в инструментальной панели и нажмем кнопку  Выйти в экран управления проектом (Дерево проекта).

                В группе функций Расчет установим курсор в позицию Линейный и нажмем левую

кнопку мыши. Если позиция Линейный имеет вид  (“выполнение невозможно”), то расчет недоступен (рис. 1.2.12). Причиной этого, как правило, является полное или частичное отсутствие обязательных исходных данных. К ним относятся: нагрузки, жесткостные характеристики и, конечно, описание геометрии расчетной схемы. В тех случаях, когда данные отсутствуют или заданы не для всех элементов схемы (последнее касается жесткостей), пиктограмма соответствующей ветви Дерева проекта в разделе Расчетная схема содержит вопросительный знак  . Если функция недоступна (например, назначение комбинаций загружений до ввода самих загружений), то ее пиктограмма в Дереве проекта включает знак “выполнение невозможно” –  . Все доступные на текущем шаге работы функции помечаются пиктограммой “действие доступно” –  .



Рис. 1.2.12. Фрагмент Дерева проекта

Рекомендуем перед выполнением расчета “пройтись” по Дереву проекта и убедиться в том, что все исходные данные, которые необходимо задать для расчета, действительно введены и попали в проект. В противном случае нужно вернуться к соответствующей функции подготовки данных и ввести недостающую информацию. 

Так как нами создана новая схема, то перед выполнением расчета автоматически выполняется операция сохранения проекта.

Не будем подробно останавливаться на функциях управления расчетом (они рассматриваются в главе 6). Дождемся сообщения о том, что процессор (рис. 1.2.13) завершил расчет и перейдем к анализу результатов.



Рис. 1.2.13. Окно Процессора

 

 

 

 

 

 



 

Графический анализ результатов расчета

После завершения расчета и указания на кнопку Выход в окне процессора управление передается Дереву проекта. Если расчет завершился успешно, а мы надеемся на такой результат, так как неоднократно считали учебную задачу, то следующим шагом будет графический анализ полученного решения. Установим курсор в позицию Графический анализ

раздела Результаты дерева проектов и нажмем левую кнопку мыши. При этом активизи­руется окно постпроцессора (рис. 1.2.14), инструментальная панель которо­го содержит различные  функции отображения результатов расчета.



Рис.1.2.14. Окно SCAD в режиме графического анализа результатов

 

Анализ перемещений

Анализ перемещений выполняется с помощью функций раздела Деформации

(рис. 1.2.15). Для этого необходимо выполнить следующие операции:

Ä    активизировать режим анализа перемещений (закладка Деформации);

Ä    выбрать в списке загружение;

Ä    выбрать направление перемещения;

нажать одну из кнопок функций отображения результатов.



Рис. 1.2.15. Инструментальная панель режима анализа перемещений (Деформации)

Набор функций отображения позволяет получить различные формы представления результатов расчета  перемещений. Каждой форме соответствует кнопка в инструментальной панели. При анализе перемещений от статических загружений в стержневых конструкциях можно воспользоваться кнопками:

  – вывод деформированной схемы на фоне исходной;

  – вывод деформированной схемы;

  – вывод значений перемещений в узлах;

  – цветовая индикация значений перемещений в узлах;

  – восстановление исходного отображения схемы.

Анализ усилий

Вы, наверное, уже обратили внимание, что независимо от режима в комплексе сохраняется преемственность функций управления. Поэтому не будем подробно останавливаться на анализе результатов расчета усилий, а только рассмотрим инструментальную панель раздела Эпюры усилий (рис. 1.2.16).





Рис. 1.2.16. Инструментальная панель режима анализа усилий

В этом режиме для анализа усилий используются кнопки:

  – вывод эпюр;

 – цветовая индикация максимальных положительных значений заданного фактора;

 – цветовая индикация максимальных отрицательных значений заданного фактора.

Печать результатов

В комплексе реализованы различные функции текстового представления результатов. В простейшем случае вывод информации на печать может выполняться в форматах редактора WordPad, который поставляется вместе с Windows 95. Для того, чтобы распечатать результаты расчета, следует перейти в Дерево

и активизировать позицию Печать таблиц раздела Результаты. В диалоговом окне Оформление результатов расчета (рис. 1.2.17) выбираем раздел, например, Перемещения и активизируем его. Здесь следует обращать внимание на у

словные обозначения, стоящие рядом с наименованием раздела. Знаком “минус” отмечаются разделы, по которым результаты отсутствуют, значок в виде компьютера показывает, что в результате расчета получена информация по данному разделу, а значок в виде принтера показывает, что формирование таблиц результатов выполнено, их можно просмотреть и распечатать.

Рис. 1.2.17. Диалоговое окно

Оформление результатов расчета

Если вам необходимо распечатать часть результатов, например, перемещения только для указанных узлов, то первой следует нажать кнопку Параметры вывода и выполнить настройку на нужные параметры.

С помощью кнопки Формирование документа выполняются операции формирования таблиц. Эту кнопку нажимаем второй.

После того, как рядом с выбранным разделом результатов появится значок “принтер”, можно нажимать на кнопку Просмотр результатов, вызывая тем самым редактор WordPad с таблицами результатов (рис.1.2.18). Чтобы редактор вызывался автоматически, необходимо выполнить назначение его вида и пути в разделе Настройка графической среды меню Опции.

Следует отметить, что существенным фактором, влияющим на представление результатов в таблицах, является выбор шрифта (Font). Удобочитаемость таблиц обеспечивают шрифты Courier  (Cyrillic) или Courier New (Cyrillic), в которых все буквы и цифры имеют одинаковую ширину (так называемый непропорциональный шрифт).





Рис. 1.2.18. Представление таблицы результатов в редакторе WordPad

Черная королева покачала головой:

Вы, конечно, можете  называть это чушью,но

 я- то встречала такую чушь, что в сравнении

  с ней  эта  кажется толковым словарем.

Л. Кэрролл “Алиса в стране чудес”

РЕЗЮМЕ

В главе SCAD для “ЧАЙНИКОВ” мы прошли путь от начала формирования расчетной схемы до вывода результатов расчета. Конечно, это был самый короткий из всех возможных маршрутов и большинство функций осталось вне нашего внимания. Но мы надеемся, что цель достигнута ? и общие принципы работы с комплексом теперь понятны.

Активизация любых функций комплекса вполняется из Дерева проекта. При подготовке исходных данных большинство операций выполняется в такой последо­вательности:

Ä    указанием на закладку установить необходимый раздел в инструментальной панели;

Ä    нажать на кнопку с пиктограммой выполняемой операции;

Ä    если для выполнения операции требуется дополни­тельная информация, надо заполнить данные в открывшемся диалоговом окне;

Ä    выбрать нужные узлы или элементы;

Ä    нажать кнопку ОК в разделе Инструментальная панель, соответствующем выбранной операции.

Для мгновенного отображения результатов работы можно включить соответствующий фильтр. Это позволяет контро­лировать процесс ввода и оперативно вносить изменения в выпол­няемые действия.

                При графическом анализе результатов рекомендуется действовать в такой последовательности:

Ä      указанием мыши на закладку установить раздел инструментальной панели с интересующей инфор­мацией (Деформации, Эпюры усилий, Поля напряжений);

Ä      выбрать нужное загружение;

Ä      выбрать вид анализируемого фактора (направ­ление перемещений или вид силового фактора) и форму графического представления резуль­татов (деформированная схема, эпюры, изополя и т.п.).



                Пришло время более подробно рассмотреть все многообразие реализованных в комплексе возможностей.

2. Создание расчетной схемы

Ознакомимся теперь с созданием расчетных схем различного вида конструкций, реализованных как параметрические прототипы, рассмотрим возможности их модификации, а также остановимся на вопросах сборки сложных расчетных схем из подготовленных фрагментов.

Большинство операций формирования этих схем сосредо­точено в разделе Схема инструментальной панели (рис. 2.1).



Рис. 2.1. Раздел Схема инструментальной панели препроцессора

В этом разделе можно выполнить:

 – рамные конструкции;

 – схемы продольного каркаса;

 – плоские шарнирно-стержневые системы;

 – плоская ортогональная сетка конечных элементов;

 – балочные ростверки;

 – типовые поверхности вращения;

 – поверхности вращения, заданные аналитически;

 – оболочки, заданные аналитически;

 – создание координационной сетки;

 – геометрические преобразования;

 – копирование схемы;

 – копирование фрагмента схемы;

 – удаление схемы;

 – сборку схемы из нескольких схем;

 – триангуляцию плоской области.

2.1 Расчетные схемы стержневых конструкций

В комплексе реализованы различные способы создания расчетных схем стержневых конструкций, в том числе: путем последовательного ввода узлов и элементов; генерации схемы по параметрическим прототипам конструкций (рамы, фермы, поверхности вращения и аналитически заданные поверхности, балочные ростверки); ввода схемы, описанной в текстовом формате на входном языке.

Пространственные многопролетные многоэтажные рамы



        В разделе 1.2 была сформирована расчетная схема плоской многопролетной многоэтажной рамы. Сейчас рассмот­рим формирование пространственных стержневых систем. В основе этой операции лежит принцип дублирования расположенной в плоскости XoZ правой декартово системы координат XYZ поперечной конструкции плоской рамы (поперечника) с заданным шагом в направлении оси Y. При этом продольные конструкции образу­ются путем порождения стержней в направлении оси Y из каждого узла поперечной конструкции. В простейшем случае, если принять, что в качестве прототипа использована сформированная нами ранее рама, то после 5-кратного дубли­ро­вания ее с шагом 6 м формируется схема, изображенная на рис. 2.1.1.



Рис. 2.1.1. Расчетная схема, полученная путем

 5-кратного дублирования рамы в направлении оси Y.

Для выполнения этой операции в разделе Схема предусмотрена специальная кнопка , при нажатии которой открывается диалоговое окно Схема продольного каркаса (рис. 2.1.2). В этом окне вводится шаг дублирования и количество повторений (шаг может быть переменным), а также назначаются жесткостные характеристики введенных в направлении оси Y стержней (кнопка Ригели). Для выполне­ния последней операции используется уже знакомое из пред­ы­ду­­щего раздела окно Жесткости стержневых элементов.

После задания данных в окне Схема продольного каркаса и нажатия кнопки ОК выполняется генерация расчетной схемы (рис. 2.1.1).

Обратите внимание, что операция дублирования выполняется только для стержневых конструкций, поперечное сечение которых сформировано с помощью параметрического прототипа. Для дублирования произвольных стержневых систем используются специальные функции, которые будут рассматриваться ниже.

Конечно, в реальном проектировании подобные регулярные конструкции встречаются редко. Для того чтобы учесть фактическую нерегулярность и модифицировать расчетную схему в комплексе, предусмотрены операции  по удалению, дополнению и переносу узлов и элементов, назначению абсолютно жестких вставок, изменению ориентации местных осей элементов и т.п. Позже мы познакомимся с ними. А сейчас продолжим рассмотрение средств создания расчетной схемы на примере одноэтажной многопролетной рамы.

Рис. 2.1.2. Диалоговое окно

Схема продольного каркаса

Рис. 2.1.3. Диалоговое окно Одноэтажная рама



Пространственные одноэтажные рамы

Вернемся к разделу Схема инструментальной панели и после нажатия кнопки Генерация прототипа рамы  выберем в диалоговом окне Выбор конфигурации рамы (см. рис. 1.2.1) тип, изображенный слева. В диалоговом окне Одноэтажная рама (рис. 2.1.3) зададим параметры расчетной схемы. Обратите внимание, что для этого класса конструкций наряду с вводом уже знакомых нам жесткостных характеристик элементов схемы и связей предусмотрена возможность задания таких данных, как уклоны ригелей, высотное и плановое положение опор подкрановых балок.



Зададим эти характеристики и сгенерируем схему, изображенную на рис. 2.1.4.

Для моделирования опирания подкрановых балок на крайних колоннах в расчетной схеме предусматривается смещение осей подкрановой части колонны относительно надкрановой части с использованием жестких вставок. На средних колоннах вводятся промежуточные узлы и выбор  способа моделирования опирания подкрановых балок (введение консолей, приведение нагрузок к центральному узлу и т.п.) остается за пользователем. Для того чтобы отобразить на схеме жесткие вставки, воспользуемся кнопкой фильтров . Так как жесткие вставки вводятся по направлению местной оси Z1

элемента, то при отключенной кнопке фильтра элементы, моделирующие надкрановую часть колонны, будут отображаться под углом.



Рис. 2.1.4. Расчетная схема поперечной одноэтажной рамы

     Рис. 2.1.5. Диалоговое окно

Схема продольного каркаса для одноэтажных рам

Аналогично тому, как мы формировали пространственную схему многоэтажной конструкции, воспользуемся кнопкой    в разделе Схема и зададим параметры дублирования поперечника. Эти операции выпол­няются в диалоговом окне (рис. 2.1.5). Обра­ти­те внимание, что в этом случае задаются жесткостные характе­ристики для двух видов стержней, связывающих поперечные рамы, если не преду­сматривается моделирование подкрановых балок, или трех видов ? если подкрановые балки введены в модель. В первом случае стержни будут соединять верхние узлы колонн и точки перегиба балок покрытия, во втором ? добавятся стержни, соединяющие узлы на отметках подкра­новых балок.

Полученная в результате схема показана на рис. 2.1.6.

Рис. 2.1.6. Расчетная схема, полученная путем 4-кратного

дублирования рамы (рис. 2.1.4) в направлении оси Y

Формирование плоских шарнирно-стержневых систем

Рис. 2.1.7. Диалоговое окно Конфигурация поясов фермы



 

 

                                                                                Рис. 2.1.8. Диалоговое окно  Параметры фермы



       Для формирования расчетной схемы фермы можно воспользоваться имеющейся в комплексе библиотекой параметрических прототипов, как нам кажется, наиболее часто используемых ферм. Выбор прототипа фермы осуществляется по двум параметрам ? очертанию поясов и схеме решетки. После нажатия кнопки в разделе Схема открывается диалоговое окно Конфигурация поясов фермы (рис. 2.1.7), в котором выбирается прототип фермы по очертанию поясов.

В этом окне следует активизировать опцию с наименованием нужного прототипа и нажать кнопку ОК. В результате откроется диалоговое окно Параметры фермы (рис. 2.1.8), где и производится окончательный выбор прототипа и задание его параметров. Если параметры фермы заданы корректно, то после нажатия кнопки ОК на экран будет выведена схема.

                Обратите внимание, что при задании параметров фермы допускается два варианта определения панелей – указанием их количества или длины. В первом случае все панели будут иметь одинаковую длину, во втором, ? если длина фермы не кратна длине панели, крайние панели укорачиваются.

В отличие от функции генерации расчетных схем по прототипам рамных конструкций при формировании шарнир­но-стержневых систем отсутствует операция назначения жесткостей элементам схемы. Это связано с разнообразием сечений эле­мен­тов в системах такого класса. Для задания жесткостей следует воспользоваться соответствующими функциями в разделе Назначение.

 

Формирование расчетной схемы балочного ростверка

Рис. 2.1.9. Генерация балочного ростверка



Для формирования расчетной схемы балочного ростверка воспользуемся соответствующей функцией в разделе Схема. Аналогично другим прототипам стержневых конструкций исходные данные для этого вида схем задаются в “своем” диалоговом окне (Рис. 2.1.9). Не будем подробно останав­ливаться на правилах задания исходных данных, так как они не отличаются от ввода характеристик рам. Отметим только, что при формировании схемы балочного ростверка предусмотрена возможность создания схем двух конфигураций – открытой по контуру и замкнутой (Рис. 2.1.10 и 2.1.11, соответственно). Выбор конфигурации схемы выполняется с помощью соответ­ствующих кнопок, расположенных в правой части окна.





Рис. 2.1.10. Пример открытого по контуру ростверка         Рис. 2.1.11. Пример замкнутого по контуру

                                                                                ростверка

Создание схемы, используемой в качестве подконструкции

            Рис. 2.1.12. Окно сообщений                              Рис. 2.1.13. Диалоговое окно Результат генерации схемы



 

Если режим формирования расчетной схемы параметрической конструкции активизируется на фоне уже существующей схемы, то появляется окно сообщений (рис. 2.1.12), в котором предлагается выбрать вариант продолжения работы:

удалить текущую схему и создать новую (кнопка Да/Yes);

использовать новую схему в качестве дополняющей подсхемы (кнопка Нет/No).

В первом случае новая схема заменяет ранее сформированную. В случае выбора второго варианта после задания параметров расчетной схемы появляется диалоговое окно Результат генерации схемы (рис. 2.1.13). В этом окне предусмотрены опции Сохранить как схему и Вызвать режим сборки. Активизация первой опции обеспечивает сохранение новой схемы в виде самостоятельного проекта, имя которого вводится в соответствующем поле. Если выбрана вторая опция, то после подтверждения назначений кнопкой ОК

автома­тически вызывается режим сборки, в котором новая схема выступает в качестве подконструкции (подсхемы) ранее созданной схемы. Обе опции можно использовать одновременно.

Плоские стержневые системы

Рассмотрим процесс формирования расчетных схем стержневых конструкций, образно говоря, с “нуля”. При этом не будут использованы применявшиеся в предыдущем разделе параметрические прототипы. Последовательно, шаг за шагом, сформируем расчетную схему, используя для этого функции ввода узлов и элементов.

Активизируем закладку инструментальной панели Узлы и элементы, где две кнопки  – Узлы и   – Элементы имеют еще незнакомое нам свойство. После нажатия одной из них в разделе раскрывается набор кнопок, управляющих работой с Узлами или Элементами. Так как ввести элементы, не привязывая их к узлам, невозможно, начнем с ввода узлов.



 

 

 

 

 

 

Ввод узлов

Рис. 2.1.14.  Диалоговое окно

Ввод узлов

       Нажмем кнопку Узлы и выберем в установившемся наборе кнопок функцию Ввод узлов. В правом верхнем углу рабочего поля открывается диалоговое окно Ввод узлов (рис. 2.1.14).

С помощью функций этого окна можно ввести один узел или группу узлов, расположенных на одинаковом расстоянии один от другого, т.е. с заданным шагом повторения. Для ввода одного узла достаточно задать его координаты в полях левой части окна и нажать кнопку Добавить. Если активен фильтр Узлы  (в противном случае вводимые узлы не будут отображаться на экране), после каждого нажатия кнопки Добавить на экране будет появляться новый узел.

Наличие повторителя позволяет вводить сразу группу узлов. Для ввода группы узлов следует:

Ä      в полях ввода координат ввести координаты первого узла группы (X, Y, Z);

Ä      активизировать режим Повторить;

Ä      ввести количество повторений в поле N;

Ä      в полях ввода приращений координат ввести значения шага повторения в одном или нескольких направлениях (dX, dY, dZ);

Ä      нажать кнопку Добавить.

Так как диалоговое окно занимает часть экрана, то в процессе ввода узлов рабочее поле экрана несколько умень­шается, что исключает попадание новых узлов под диалоговое окно. После завершения операций ввода следует нажать кнопку Закрыть. Диалоговое окно закроется и изображение будет вновь занимать все рабочее поле. Ограничений на коли­чество обращений к функции Ввод узлов нет. Если операцию надо повторить, следует опять нажать на кнопку Ввода узлов в инструментальной панели. После того, как все или часть узлов введены, можно приступить к вводу элементов.

Ввод элементов

Рис. 2.1.15.  Расчетная схема трехпролетной одноэтажной рамы

        Нажмите кнопку Элементы и тем самым раскройте набор кнопок, управляющих работой с элементами. Для ввода стержневых элементов используется кнопка Ввод стержней. Активизируйте эту кнопку и установите курсор с мишенью на первый узел вводимого элемента. Нажмите левую кнопку мыши и протяните “резиновую нить” до второго узла. Вторичным нажатием левой кнопки в области второго узла зафиксируйте ввод элемента. Последовательно повторяя описанные выше действия, введите другие элементы.



Если в процессе ввода возникнет проблема точного указания курсором на узел, то прицел курсора можно “загрубить”. Для этого, нажав на правую кнопку мыши, вызовите окно Выбор узлов и элементов (см. рис. 1.2.8) и в группе кнопок установки точности назначьте новое значение, отличное от нуля (см. раздел Выбор узлов и элементов в главе 3).

               Сейчас, основываясь на полученной информации, попробуем создать простую расчетную схему из стержневых элементов, например, трехпролетную одноэтажную раму, изображенную на рис. 2.1.15.

В приведенной ниже таблице иллюстрируется порядок выполнения операций в диалоговом окне Ввод узлов (см. рис. 2.1.14), который был использован при формировании этой схемы.

X	Y	Z	Признак	dX	dY	dZ	N	Действие
0.0	0.0	0.0	Повторить	24.0	0	0	3	Добавить
0.0	0.0	12.2	Повторить	24.0	0	0	3	Добавить
24.0	0.0	15.2	–					Добавить
48.0	0.0	15.2	–					Добавить

После задания узлов можно перейти к вводу элементов. При вводе вертикальных стержневых элементов желательно придерживаться такого порядка отметки узлов, при котором первым назначается нижний узел. В этом случае местная ось элементов Х1

будет направлена вверх.

Вы, наверное, обратили внимание, что при формировании схемы использовались только две из множества функций раздела Узлы и Элементы. Здесь не ставилась цель изучения этих функций. Им будет уделено особое внимание, так как с их помощью можно сформировать и модифицировать схемы самых сложных конструкций.

2.2 Расчетные схемы конструкций из пластинчатых элементов

В настоящем разделе рассмотрены функции формирования расчетных схем из плоскостных конечных элементов. К ним относятся формирование прямоугольной и треугольной сеток конечных элементов на плоскости.

Формирование прямоугольной сетки конечных элементов на плоскости

Рис. 2.2.1. Диалоговое окно

Генерация пластинчатой схемы

       С помощью этой функции может быть создана прямоугольная сетка с переменным или постоянным шагом, расположенная в плоскости XoY или XoZ. Назначение параметров сетки выполняется в диалоговом окне, изображенном на рис. 2.2.1.



Тип схемы и ее положение в пространстве назначаются с помощью кнопок, установленных в верхней части окна. При правильном выборе типа схемы конечным элементам автоматически будет назначен тип и его не придется изменять в процессе работы со схемой. Плитам по умолчанию назначается тип 11, балкам–стенкам – 21, оболочкам  – 41. Если для конкретной конструкции предпочтительным является другой тип элемента, то он может быть назначен с помощью кнопки Тип элемента в диалоговом окне Назначение типа элемента (см. рис. 1.2.6). Для генерации схемы введем в таблицу параметры разбивки по двум направлениям, а также жесткостные характеристики элементов (кнопка Жесткость). Работа с диалоговым окном назначения жесткостей пластинчатым элементам описывается в разделе 4.1.

В качестве примера рассмотрим генерацию плиты,  10*5 м с шагом сетки 1м по обоим направлениям. Для этого зададим шаг 1м по направлению Х, количество шагов – 10, а также шаг 1м по направлению Y, количество шагов – 5. После нажатия кнопки ОК будет сформирована схема, показанная на рис. 2.2.2.

               

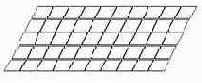
Рис. 2.2.2. Прямоугольная плита с постоянным шагом сетки конечных элементов

При формировании сетки с разным шагом вводятся величины шагов и количество повторений по каждому направлению. Если в предыдущем примере изменить величину шага в направлении Х на 0.5 м, получим схему, изображенную на рис. 2.2.3.



Рис. 2.2.3. Схема плиты с разным шагом сетки вдоль осей Х и Y

И, наконец, рассмотрим случай, когда вдоль осей задан переменный шаг сетки (рис. 2.2.4). В качестве примера зададим следующие параметры разбивки:

Шаг вдоль оси Х	Количество шагов	Шаг вдоль оси Y	Количество шагов
0.5	6	0.25	8
0.25	8	0.5	6
1	5

При назначении разного шага сетки следует помнить, что наиболее качественное решение будет получено при соотно­шении сторон четырехузловых конечных элементов близким к 1. Не рекомендуется назначать соотношение более 1/5. Идеальным в этом смысле является квадрат.



Рис. 2.2.4. Схема плиты с переменным шагом сетки вдоль осей Х и Y

Формирование треугольной сетки конечных элементов на плоскости

Автоматическая триангуляция замкнутой области произвольной формы на плоскости является одним из наиболее универсальных средств формирования сеток конечных элементов. В комплексе предусмотрена возможность использовать триангуляцию как для создания новой схемы, так и для триангуляция фрагмента уже готовой схемы. Рассмотрим случай создания новой схемы.

Перед тем, как выполнить триангуляцию, необходимо ввести узлы, через которые проходит контур, ограничивающий область триангуляции и, если это необходимо, внутренние контуры, в которых триангуляция не выполняется, например, отверстий. Для выполнения этой операции воспользуемся кнопкой Ввод узлов –  и зададим узлы внешнего контура со следующими координатами:

№ узла	X	Y	Z
1	0.0	0.0	0.0
2	20.0	0.0	0.0
3	20.0	12.0	0.0
4	32.0	12.0	0.0
5	32.0	24.0	0.0
6	0.0	24.0	0.0
Аналогично введем узлы внутренних контуров:
7	3.0	3.0	0.0
8	12.0	3.0	0.0
9	12.0	9.0	0.0
10	3.0	9.0	0.0
11	15.0	12.0	0.0
12	17.0	12.0	0.0
13	17.0	15.0	0.0
14	28.0	15.0	0.0
15	28.0	19.0	0.0
16	15.0	19.0	0.0

Положение и номера введенных узлов показаны на рис. 2.2.5. После ввода узлов активизируем в разделе Схема

функцию Формирование треугольной сетки конечных элементов на плоскости. В результате в инструментальной панели станут доступны кнопки управления режимом триангуляции,  изображенные на рис. 2.2.6.

Для триангуляции заданной области необходимо выполнить следующую последовательность операций:

Ä      нажать кнопку Задание контура  и обвести “резиновой нитью” опорные узлы внешнего контура (под “опорными” понимаются узлы, лежащие в угловых точках контура);



Ä      нажать кнопку Задание контура и обвести “ резиновой нитью” опорные узлы внутреннего контура;

Ä      повторить предыдущую операцию для всех внутренних контуров (рис. 2.2.7);

Ä      нажать кнопку Генерация сетки конечных элементов  и установить в диалоговом окне параметры триангуляции (рис. 2.2.8);

Ä      после выхода из диалогового окна нажатием кнопки ОК выполняется разбиение заданной области на треугольные конечные элементы (рис. 2.2.9).

Остановимся подробнее на особенностях ввода контура:

при вводе участка контура можно не останавливаться на узлах, лежащих на прямой, соединяющей опорные узлы. Они будут введены в контур автоматически;

замыкание контура выполняется двойным щелчком мыши после ввода последнего узла или указанием на первый узел;

не допускается наличие совпадающих узлов как опорных, так и промежуточных (здесь и далее под совпадающими будем понимать узлы, имеющие одинаковые координаты);

не допускается попадания внутрь контура совпадающих узлов;

не допускается наличие внутри контура узлов, лежащих от контура на расстоянии менее 0.15 заданного шага триангуляции, так как это приведет к появлению вырожденных треугольников;

внутренние контуры не должны пересекать или касаться наружного контура и один другого;

не допускается наличие контуров, лежащих вне контура, ограничивающего область триангуляции;

введенный контур можно сохранить, нажав кнопку Сохранение контура . Если к моменту сохранения задано несколько контуров, то все они сохраняются под одним именем. Как правило, удобнее сохранять каждый контур отдельно. Для этого после ввода и сохранения контура следует нажать кнопку Отказ и только после этого вводить новый контур. Перед выполнением триангуляции необходимо нажатием кнопки Отказ

очистить схему от всех контуров, затем последовательно вызвать контуры из списка, расположенного справа от кнопки сохранения, и активизировать операцию Генерация сетки конечных элементов .



Рис. 2.2.5. Узлы, ограничивающие внешний и внутренние контуры области триангуляции



Рис. 2.2.6. Кнопки управления режимом триангуляции

Рис. 2.2.7. Назначение контуров





Рис. 2.2.8. Диалоговое окно

Автоматическая триангуляция

Перед выполнением триангуляции в окне Автома­тическая триангуляция (см. рис. 2.2.8) нужно выбрать метод триангуляции. Здесь также можно задать жесткостные характе­ристики конечных элементов (для этого используется кнопка Жесткости).

В соответствии с выбранным методом триангуляция может быть выполнена:

только на заданных узлах,

с разбивкой области триангуляции с заданным шагом вдоль координатных осей, но без ввода дополнительных узлов на участках контура,

с разбивкой и контура и области триангуляции в соответ­ствии с заданным шагом

Если в диалоговом окне Автоматическая триангу­ляция установлен признак объединения трехузловых элементов в четырехузловые, то в процессе формирования схемы такое объединение будет выполнено для всех допустимых пар треугольников.

                Схема, созданная в результате триангуляции, фактически является самостоятельной подсхемой, и после завершения триангуляции ее нужно “установить на место”, т.е. присоединить к узлам, на которых выполнялась триангуляция (кнопка  – Установка сформи­ро­ванной схемы по месту).

Если подсхему предполагается присоединять к другим фрагментам схемы, ее можно сохранить и как самостоятельную схему, воспользовавшись для этого кнопкой  Запись результатов триангуляции. При этом схема должна быть записана под новым именем, отличным от имени основной схемы.

                В отличие от создания новой схемы, триангуляция области, принадлежащей уже существующей расчетной схеме, выполняется путем задания контура непосредственно на исходной схеме или ее фрагменте. После завершения триангуляции полученная схема может быть сохранена как самостоятельная схема (кнопка Запись результатов триангуляции), установлена по месту в схему (кнопка Установка сформированной схемы по месту) или выполнены обе эти операции.



Окончательная фиксация результатов триангуляции выполняется только после выхода из режима триангуляции (отжата кнопка Формирование треугольной  сетки конечных элементов на плоскости). В этом случае на экран выводится результирующая расчетная схема. В течение одного “сеанса” мож­но выполнить триангуляцию только одной области, затем закрыть режим триангуляции. Для триангуляции другой области следует снова активизировать режим триангуляции.



 

Рис. 2.2.9. Расчетная схема, полученная в результате выполнения триангуляции

 

                 Некоторые "тонкости"

 Если в результате триангуляции создана новая схема, то ее присоединение к основной схеме выполняется в режиме Сборка (см. раздел 2.6).

Если в область триангуляции попали стержневые элементы, включая контурные, то их следует предварительно разбить на ряд элементов по длине в соответствии с предполагаемым шагом триангуляции;

перед выполнением триангуляции выполняется порождение узлов вдоль стержневых элементов, находящихся в области триангуляции и на контуре. Эти узлы учитываются при выполнении триангуляции, что исключает пересечение стержня пластинами. Однако, автоматическое дробление

стержней на ряд элементов не выполняется. Эту операцию можно выполнить после триангуляции, воспользовавшись функцией Добавление стержней с учетом промежу­точных узлов в разделе Узлы и Элементы, после чего удалить ранее заданные стержни;

все узлы, попавшие в область триангуляции и не принадлежащие области внутренних контуров, будут учтены при формировании сетки;

триангуляция не выполняется если в области триангуляции есть совпадающие узлы или стержневые элементы, у которых один из узлов лежит вне этой области;

если по какой-либо причине необходимо повторить ввод контура, то перед этим надо обязательно нажать на кнопку   – Отказ, в противном случае будет выдано сообщение об ошибке.

2.3 Поверхности вращения

Рис. 2.3.1. Диалоговое окно

Создание поверхности вращения

Здесь рассмотрены операции создания расчетных схем или их фрагментов, моделируемых с помощью стандартных поверхностей вращения. В комплексе преду­смотрена возможность создания схем в виде цилиндра, конуса, сферы и тора. При этом термин “поверхности” может показать­ся не совсем точным, так как схемы можно создавать и из стержневых элементов, узлы которых лежат на этой поверхности.



Рассмотрим диалоговое окно Создание поверхности вращения, в котором назначается вид поверхности и задаются ее  характеристики (рис. 2.3.1). Характеристики схемы содержат: вид элементов (стержни, пластины), форму сетки элементов (для стержневых элементов – решетки), размеры и другие данные, необходимые для генерации поверхности.

                В процессе задания параметров схемы могут быть назначены типы элементов и их жесткости. По умолчанию для стержней принят тип 5, а для пластин – 42 (треугольники) или 44 (четырехугольники).

Ниже приведены правила подготовки исход­ных данных при формировании различных схем поверх­ностей вращения.

Порядок выполнения операций назначения характеристик поверхности вращения:

Ä      выбрать вид поверхности;

Ä      выбрать вид элементов схемы;

Ä      назначить тип разбивки;

Ä      ввести геометрические характеристики;

Ä      назначить жесткостные характеристики элементов (этот шаг целесообразно выполнять, если все или большинство элементов имеют одинаковые характеристики);

Ä      нажать кнопку ОК.

Ввычисление  радиуса по хорде



Рис. 2.3.2. Диалоговое окно Вычисление радиуса по хорде

В тех случаях, когда при описании цилиндра, конуса или сферы  задание длины грани (хорды) предпочтительнее, чем задание радиуса поверхности, можно воспользоваться операцией вычисления радиуса, как функции от количества граней и длины хорды. В этом случае необходимо задать коли­чество граней (nR - количество элементов в основании цилинд­ра или конуса, а для сферы - по экватору) и нажать кнопку вызова диалогового окна Вычисление радиуса по хорде (рис. 2.3.2), расположенную слева от поля ввода радиуса.

В этом окне следует ввести длину хорды и нажать кнопку Вычислить. После нажатия кнопки Применить

окно закрывается, а результат автоматически переносится в соответствующее поле ввода окна Создание поверхности вращения.

Рекомендации по применению проектно-вычислительного комплекса SCAD в практических расчетах

 

В этом разделе приведены краткие сведения о подходах к расчету и методах решения задач, положенных в основу комплекса SCAD. Они излагаются лишь в той степени, в которой это полезно знать пользователю для лучшего понимания дальнейших указаний и для анализа ситуаций, возникающих в процессе решения конкретной задачи. Приводимые сведения не заменяют знакомство со специальной литературой, на которую даются ссылки в тексте, но могут служить некоторым путеводителем по этой литературе.

                Опыт выполнения расчетов самых разнообразных конструкций свидетельствует о наличии ряда затруднений, для преодоления которых разработаны эффективные практические приемы. Эти затруднения касаются проблемы адекватного отображения конструкции в расчетную модель, выбора подходов к дискретизации двухмерных (пластины, оболочки) и трехмерных (массивные тела) фрагментов, учет таких особенностей конструкции как наличие узловых эксцентриситетов, упругоподатливых соединений и др. Далее представлен анализ некоторых из упомянутых проблем и даны практические рекомендации расчетчику, использующему программно-вычислительный комплекс SCAD. Естественно, что читатель не найдет здесь ответа на любой вопрос, который может возникнуть в его расчетной практике, однако и относительно краткий набор рецептов может оказаться полезным, поскольку отобраны достаточно типичные ситуации.

19. Теоретические основы

19.1. Конструкция и ее расчетная схема

19.1.1. Общие сведения

                Расчетный анализ любой конструкции начинается с попытки установить, что именно в рассматриваемом случае является существенным, а чем можно пренебречь. Такого рода упрощение задачи производится всегда, поскольку выполнение расчета с учетом всех свойств реальной конструкции возможно лишь с определенной степенью приближения.

                Реальная конструкция, освобожденная от всех несущественных особенностей и представленная в связи с этим в некоторой идеализированной форме, носит название расчетной схемы. Некоторые методы схематизации получили широкое распространение и имеют общий характер (идеализация материала в виде сплошной среды; предположение об однородности материала; приведение геометрической формы тела к таким стандартным схемам, как стержни, пластины или оболочки; схематизация внешних сил и др.). Другие методы схематизации вполне конкретны и связываются с каждой рассматриваемой задачей. Однако во всех случаях выбор расчетной схемы является важнейшим элементом анализа, одной из наиболее характерных черт инженерного искусства (здесь – именно искусства, а не научного анализа!) и характеризует уровень профессионального мастерства расчетчика.

Как и любому другому виду искусства, искусству выбора расчетных схем можно научить только в процессе практической работы. Поэтому далее этой стороне проблемы мы больше не будем уделять внимание*.

Однако, после того как расчетная схема (быть может лишь в общих чертах) установлена, наступает период ее детального описания в форме, пригодной для выполнения расчетного анализа, и уже этому этапу далее посвящены конкретные рекомендации.

                Что же касается общих сведений, то следует иметь в виду, что на достаточно ранних стадиях создания расчетной схемы следует принять решение о том, будет ли расчет выполняться как линейный или как нелинейный, следует ли учитывать силы инерции и выполнять динамический расчет или же можно ограничиться статическим

анализом.

                Об ожидаемом поведении конструкции судят на основании имеющегося опыта и инженерной интуиции и поэтому все принятые решения подлежат апостериорной оценке. Если во всех разрешающих уравнениях, описывающих поведение системы, могут быть проигнорированы производные по времени, то речь идет о статической задаче и, следовательно, об анализе поведения неподвижной системы. В задачах динамики, когда существенную роль играют силы инерции, пропорциональные ускорениям масс, и в задачах ползучести, когда учитываются скорости, речь должна идти об анализе движущейся системы.

                Нелинейные задачи могут быть связаны с эффектами, возникающими при изменении геометрии системы под нагрузкой (геометрическая нелинейность), отсутствием пропорциональности между напряжениями и деформациями (физическая

нелинейность), с возможным включением и выключением из работы односторонних связей при действии нагрузки на систему (конструктивная нелинейность) или с эффектами, определяемыми переменностью структуры системы в процессе ее создания (генетическая нелинейность).

                Все указанные особенности ожидаемого поведения конструкции сказываются на выборе расчетной схемы, например, при определении возможных степеней свободы или при схематизации нагрузок, действующих на систему.



                Особенно серьезным вопросом является разбиение системы на конечные элементы, т.е. на стандартные части, из которых (и только из них!) должна состоять вся система.

                Чрезмерно мелкое дробление приводит к росту времени расчета и связано с запросом на использование больших ресурсов памяти ЭВМ для хранения и обработки данных. Могут при этом проявляться и эффекты неустойчивости самого процесса расчета. Слишком грубое дробление может привести к потере точности результатов, в особенности для тех случаев, когда рассчитываются пластинчатые или оболочечные конструкции.

                Общих рекомендаций по выбору оптимального уровня дробления системы на конечные элементы не существует. Имеющиеся “оценки сходимости” имеют асимптотический характер (см., например, [8]) и часто являются слишком абстрактными для конструктивного использования в конкретном случае расчета. Поэтому здесь приходится полагаться, главным образом, на накопленный опыт и на результаты некоторых контрольных расчетов, выполняемых для одной и той же конструкции при различных системах разбиения на конечные элементы. Могут быть также рекомендованы приемы последовательной серии расчетов некоторых фрагментов системы с введением на этих фрагментах более детального разбиения на конечные элементы.

Сейсмика

                В основу норм [24] положен спектральный подход, в соответствии с которым расчетная спектральная кривая (закон изменения коэффициентов динамичности) определяет динамическую реакцию простого маятника на ускорение точки подвеса при сейсмическом возмущении.

                В общем случае при ускорениях основания сооружения d2zo/dt2, происходящих при землетрясении, инерционные силы (19.11) определяются абсолютными ускорениями, которые суммируются с относительными ускорениями от деформации сооружения

                                                                Jc(t) = M(d2Z/dt2 - d2zo/dt2),                                                                                  (19.33)

что при подстановке в (19.12) дает фиктивную нагрузку

                                                                         fc(t) = M d2zo/dt2 .                                                                                           (19.34)

От воздействия (19.34) решение ищется путем разложения по формам собственных колебаний в форме интеграла Дюамеля (см. раздел 3 справочника [5]) и в конце концов приводится к расчету на инерционные силы  Sik, действующие по направлению k-ой

массы при колебаниях по i-ой форме

                                                                   Sik = QkKcb(Ti)hikcosjok.                                                                                     (19.35)

Здесь Qk

– вес k-ой массы; Kc – коэффициент сейсмичности, зависящий от бальности землетрясения (напоминаем, что переход к следующему баллу связан с удвоением мощности землетрясения) и от класса сооружения; b – коэффициент динамичности, зависящий от периода собственных колебаний рассматриваемой формы и определяемый по формуле

                                                                          b = a/T    (b £ b),                                                                                            (19.36)

где константы a и b связаны с категорией грунта основания; hik – приведенные ускорения (19.30); jok – угол между направлением сейсмического толчка и смещением Zk.

От нагрузок (19.35) определяются отклики Xi

для каждой из учитываемых форм колебаний, затем находится максимальный из них Xa = maxiïXiïи определяется расчетное значение

                                                                   X = [X2a ±

]1/2.                                                                                     (19.37)

Сходимость МКЭ

В теории метода конечных элементов большое внимание уделяется проблеме сходимости, т.е. асимптотическому поведению оценок точности получаемого приближенного решения при неограниченном сгущении сетки конечных элементов. Установлен ряд важных теорем о сходимости, например, для совместных элементов определено [26, стр. 195-196], что если (k-1) является степенью полинома, с помощью которого внутри конечных элементов аппроксимируется перемещение и решается эллиптическая краевая задача порядка 2m, для которой получено приближенное решение в перемещениях u*, то ошибка в энергии по сравнению с точным решением u составляет

U(u-u*, u-u*) £ C2h2(k-m)||u||2k ,

где h – максимальное значение относительного размера элемента (шаг сетки).

Для  s-х производных z имеем оценки ошибок

||z-z*||s £ Chk-s||z||k  ,   если s > 2m-k ;

||z-z*||s

£ Ch2(k-s)||z||k ,   если s £ 2m-k.

Для несовместных элементов аналогичные оценки получены в серии работ И.Д. Евзерова и В.С. Карпиловского (см., например, [8], [13]). Используя эти результаты можно получить оценки сходимости для всех конечных элементов из библиотеки SCAD, которые представлены в таблице 20.1.

Таблица 20.1.   

Тип		Наименование конечного элемента		Показатель степени в оценках скорости сходимости по:
КЭ				ïåðåìå­ùåíèÿìперемещениям		íàïðÿæå­­íèÿìнапряжениям		ìîìåí­òàìмоментам		ïîïåðå÷­íûì ñèëàìпоперечным силам
11,13		Универсальный прямоугольный элемент плиты		2		—		2		1
12,14		Универсальный треугольный элемент плиты		2		—		1		0
20		Универсальный четырехугольный (от 4 до 8 узлов) элемент плиты		2		—		1		0
21		Универсальный прямоугольный элемент плоской задачи теории упругости		2		1		—		—
22		Универсальный треугольный элемент плоской задачи теории упругости		2		1		—		—
23		Универсальный прямоугольный элемент плоской задачи теории упругости		2		1		—		—
24		Универсальный треугольный элемент плоской задачи теории упругости		2		1		—		—
27		Универсальный четырехугольный (от 4 до 8 узлов) элемент плоской задачи теории упругости		2		1		—		—
29		Универсальный четырехугольный (от 4 до 12 узлов) элемент плоской задачи теории упругости		2		1		—		—
30		Универсальный четырехугольный (от 4 до 8 узлов) элемент плоской задачи теории упругости		2		1		—		—
31		Параллелепипед		2		1		—		—
32		Тетраэдр		2		1		—		—
33		Трехгранная призма		2		1		—		—
34		Пространственный изопараметрический шестиузловой элемент		2		1		—		—
36		Пространственный изопараметрический восьмиузловой элемент		2		1		—		—
37		Пространственный изопараметрический двенадцатиузловой элемент		2		1		—		—
41		Универсальный прямоугольный элемент оболочки		2		1		1		0
42		Универсальный треугольный элемент оболочки		2		1		1		0
44		Универсальный четырехугольный элемент оболочки		2		1		1		0
50		Универсальный четырехугольный (от 4 до 8 узлов) элемент оболочки		2		1		1		0
61		Универсальный кольцевой элемент с прямоугольным поперечным сечением		2		1		—		—
62		Универсальный кольцевой элемент с треугольным поперечным сечением		2		1		—		—
64		Универсальный кольцевой элемент с прямоугольным поперечным сечением (от 4 до 8 узлов)		2		1		—		—
71		Прямоугольный элемент многослойной оболочки (учет поперечного сдвига, обжатия слоев, кривизны)		2		1		—		—
72		Треугольный элемент многослойной оболочки (учет поперечного сдвига, обжатия слоев, кривизны)		2		1		—		—
73		Четырехугольный элемент многослойной оболочки (учет поперечного сдвига, обжатия слоев, кривизны)		2		1		—		—
74		Четырехугольный (от 4 до 8 узлов) элемент многослойной оболочки (учет поперечного сдвига, обжатия слоев, кривизны)		2		1		—		—
81		Прямоугольный элемент многослойной оболочки (учет межслоевых сдвигов и кривизны)		2		1		—		—
82		Треугольный элемент многослойной оболочки (учет межслоевых сдвигов и кривизны)		2		1		—		—
83		Четырехугольный элемент многослойной оболочки (учет межслоевых сдвигов и кривизны)		2		1		—		—
84		Четырехугольный (от 4 до 8 узлов) элемент многослойной оболочки (учет межслоевых сдвигов и кривизны)		2		1		—		—

Данные, представленные в таблице 20.1, дают возможность приблизительно назначить требуемую густоту сетки конечных элементов, исходя из такого весьма характерного рассуждения [3, стр.55]: "... заметим лишь, что при естественных ограничениях на исходные данные и сетку области, сходимость имеет место и погрешность в определении напряжений и деформаций имеет порядок ch/L, где через с

обозначена константа, зависящая от формы области; h

— шаг сетки; L — характерный размер области. Эта оценка служит ориентиром при назначении шага сетки в зависимости от желаемой точности (средней), например, задав точность приближенного решения 5%, нужно выбрать шаг сетки равным примерно 1/20 от характерного размера...", т.е. для характерного двумерного пятна необходимо иметь около 400 узлов, а в трехмерной задаче – примерно 8000.

Спектры ответа

14.1 Расчет на сейсмические воздействия

Выведенный из положения равновесия линейный неконсервативный осциллятор совершает затухающие колебания, которые описываются дифференциальным уравнением

                                                                 (14.1)

где

                w – собственная круговая частота системы без затухания (рад/с);

                j – относительное демпфирование. При j < 1 решение уравнения (1) имеет вид

где

               

 – частота с учетом затухания,

                А, a – коэффициенты, которые зависят от начальных условий.

                Обычно для строительных конструкций j<<1 и практически

.

                Если на массу действует сила F(t), то ее перемещения описываются уравнением

                                                   (14.2)

общее решение которого при нулевых начальных условиях можно записать с помощью интеграла Дюамeля

                  (14.3)

                При движении основания с ускорением

 (кинематическое возмущение) на массу m действует переносная сила инерции . Поэтому уравнение, описывающее относительные перемещения массы в системе координат, связанной с основанием, имеет вид

,                                                        (14.4)

а его решение

                               (14.5)

                При определении абсолютного ускорения массы

 получаем при обычных малых значениях j, что

(14.6)

                Нами рассматриваются колебания линейных дискретных систем со многими степенями свободы, полученные из любых континуальных или комбинированных систем после применения к ним процедуры дискретизации метода конечных элементов (МКЭ). При этом решается система обыкновенных дифференциальных уравнений

                                                                 (14.7)

где          {u} – вектор перемещений;

                [M] – матрица массы;

                [K] – матрица жесткости.

Вынужденные колебания линейной дискретной системы с затуханием по гипотезе Фойгта-Кельвина описываются системой обыкновенных дифференциальных уравнений

,                                            (14.8)

где          [C] – матрица диссипации энергии;

                {F(t)} – вектор нагрузки.

                В случае кинематического возмущения в качестве нагрузки выступают переносные силы инерции и система уравнений (14.8) записывается в виде

,                               (14.9)

где          {u} – вектор относительных перемещений (например, в системе координат xOy, связанной с основанием);

                {I} – вектор, компонентами которого являются косинусы углов между направлениями перемещений по координатам и вектором ускорения основания;

                - ускорение основания.

                Решение уравнения (14.9) отыскивается в виде разложения его по формам собственных колебаний системы (так называемая “модальная суперпозиция”)

,                                                                    (14.10)

где          n – число степеней свободы системы (учитываемых собственных чисел и векторов);

                 – j-я форма собственных свободных колебаний дискретной системы;

                 – неизвестные функции времени, которые необходимо определить.

                Будем предполагать, что для матрицы диссипации [С] выполняется условие



где wi – i-я собственная частота дискретной системы.

                После подстановки (14.10) в (14.9) и умножения (14.9) на вектор  для нахождения  получаем дифференциальное уравнение

,                                   (14.11)

где         

                Для определения инерционных нагрузок на конструкцию необходимо знать абсолютные ускорения ее точек:



             Сейсмические колебания дискретных систем описываются системами дифференциальных уравнений (8) с несколько более общим видом правой части:

,     (14.12)

где          и  – компоненты расчетной акселерограммы. Если какая-либо из компонент не учитывается, то соответствующая часть нагрузки из (14.12) исключается.

14.2 Поэтажные акселерограммы и спектры ответа

При анализе сейсмостойкости оборудования необ­ходимо определить действующие на него инерционные сейс­мические нагрузки. Принят метод раз­дель­ного рассмотрения сейсмических колебаний здания и обо­ру­дования с использованием так называемых поэтажных аксе­лерограмм и поэтажных спектров ускорений – акселе­рограмм и спектров, рассчитанных для точек крепления оборудования.



                Расчет производится следующим образом:

определяются (вычисляются) вынужденные коле­ба­ния сооружения при сейсмическом воздейст­вии, заданном расчетной акселерограммой на грунте;

определяются законы изменения абсолютных ускорений выбранных точек конструкции;

принимая акселерограммы в качестве возмущающего воздействия, рассчитывают вы­нуж­ден­ные линейные колебания линейных некон­сер­вативных осцилляторов, и находят зависимость модулей их максимальных абсолютных уско­рений от их собственных частот и коэффициентов диссипации.

Таким образом, для каждой исследуемой точки решается уравнение (2), в котором:

зафиксирован коэффициент диссипации j;

нагрузкой является вычисленное возмущающее воздействие от расчетной акселерограммы;

наборы собственных частот осциляторов при расчете спектра ответа зафиксированы и приведены в таблице 14.1.

Таблица 14.1.

Частотный диапазон (гц)	Приращения (гц)
0.2 – 3.0 3.0 – 3.6 3.6 – 5.0 5.0 – 8.0 8.0 – 15.0 15.0 – 18.0 18.0 – 22.0 22.0 – 34.0	0.10 0.15 0.20 0.25 0.5 1.0 2.0 3.0

К приведенным в табл. 14.1 значениям частот неконсервативных осцилляторов добавляются еще собственные частоты рассчитываемой конструкции. Это делается для того, чтобы учесть возможность резонанса с ними.

                Для каждого указанного осцилятора находятся решения на всем диапазоне действия акселерограммы и выбирается максимальное по абсолютной величине, которое и является спектром ответа данной точки на действие данной акселерограммы.

14.3 Ввод данных и анализ результатов

Окно постпроцессора Спектры ответа (рис. 14.3.1) содержит список с номерами узлов, для которых необходимо вычислить спектры ответа (Список узлов). Имена акселерограмм, по которым необходимо выполнить расчет спектров, выбираются из списка имеющихся (Исходные) и переносятся в список используемых в расчете (Выбранные) с помощью кнопки Добавить. Если случайно выбрана не та акселерограмма, то ее можно убрать из списка Выбранные



кнопкой Вернуть. Кроме того для расчета необходимо установить направление действия, ввести коэффициент диссипации (в диапазоне от 0 до 1) и, если это необходимо, задать коэффициенты диссипации по формам (например, для

4-х форм следует ввести через пробел четыре числа). Если введено меньше значений, чем задано форм, то последнее введенное значение будет отнесено ко всем последующим формам.

                Выбор загружений, для которых выполняется расчет, осуществляется в списке, размещенном в нижней части экрана.

                Расчет выполняется после подготовки всех данных нажатием кнопки ОК. После окончания расчета открывается доступ к кнопке Результаты.

                Просмотр результатов и их документирование выполняется в диалоговом окне Результаты. Для построения спектров необходимо назначить номер узла, номер загружения и имя акселерограммы. Программа позволяет получить на одном графике спектры по одному или нескольким направлениям, во всем диапазоне частот или в заданном. Полученные графики и результаты расчета могут быть выведены на принтер кнопками Печать графиков и Результаты (таблицы) соответственно.



Рис. 14.3.1. Диалоговое окно

          Спектры ответа



Рис. 14.3.2. Диалоговое окно Результаты

 

 

 

 

 

 

 

 

14.4 Подготовка файлов акселерограмм

Файлы акселерограмм находятся в корневом каталоге ПВК SCAD и имеют расширение SPC. При передаче пользователям постпроцессора поставляются для примера четыре стандартные акселерограммы.

                Рассмотрим пример задания акселерограммы:

Расчетная акселерограмма в cм/(c*c) для ПЗ  на площадке атомного реактора.

Компонента  –  SH.  Mодель – 1c.  Amax =  45.1 cм/(c*c).

Количество точек N =  2047; Шаг по времени Dt =  0.05000 c.

                #

                0.01 2047 0.05

0.0     0.0     0.1     0.3     0.4     0.6     0.5     0.0    –2.1    –2.6 …

               

После символа # следуют:

коэффициент перевода заданных ускорений в м/ceк2 ;

количество точек;

шаг по времени;

значения ускорений.

                Аналогичным образом может быть подготовлен файл с нужной акселерограммой (файл с расширением SPC следует поместить в каталог с исходными данными). Для использования акселе­рограмм, поставляемых в составе комплекса, соответствующие файлы необходимо скопировать из каталога SCAD в каталог с исходными данными.

Справка

Раздел Справка содержит пункты меню, позволяющие полу­чить справочную информацию о комплексе в целом и подроб­ную информацию о подготовке исходных данных, чтении результатов, управлении режимами и т.п. Кроме того в этом разделе выполняется перерегистрация – ввод нового кода ключа защиты.

Меню препроцессора и постпроцессора

Меню состоит из пяти разделов – Проект, Файл, Опции, Операции, Сервис и Справка.

Стержни

                В качестве критерия определения РСУ здесь приняты экстремальные значения нормальных и касательных напряжений в контрольных точках сечения (рис. 19.4).

Рис. 19.4

Для нормальных напряжений используется формула: ,                                     (19.44) где: k – точка сечения стержня (k = 1 ¸ 9). Эта формула преобразуется следующим образом при  и   ,                                      (19.45) где ly,i и lz,i ядровые расстояния в сечении стержня (i=1,2).

Такой подход позволяет определить экстремальные нормальные напряжения в сечении любой формы.

Для касательных напряжений используется приближенная формула:

                                                          

.                                                                             (19.46)

Кроме напряжений вычисляются также экстремальные значения продольной и перерезывающих сил. Всего для сечения стержня отбирается 30 значений РСУ.

Учет дополнительных связей

                Если перемещения Z стеснены условиями связи

                                                                                  CZ = 0,                                                                                                      (19.8)

то только часть компонент вектора Z допускает свободное варьирование, и для учета этих связей в работе [17] было предложено использовать модифицированную функцию Лагранжа

                                                      ÏLÌ =  1/2ZT(K + CTDoC)Z - ZTf + rT CZ,                                                                          (19.9)

в которой Do есть некоторая симметричная положительно определенная матрица, а r – вектор Лагранжевых множителей (реакций в связях).

                Условия стационарности функционала (19.9) дают систему уравнений

                                                                 KZ + (CTDoC)Z + C Tr =  f;

                                                                                  CZ = 0.                                                                                                    (19.10)

                Следует отметить, что матрица С должна содержать только линейно независимые строки, в противном случае (постановка дублированных связей) в системе может оказаться статически неопределимая подконструкция, целиком состоящая из абсолютно жестких элементов, что ведет к вырождению задачи. Во всех остальных случаях система уравнений (19.10) имеет отличный от нуля определитель, включая и те случаи, когда матрица К вырождена (конструкция без дополнительных связей изменяема), но ее дефект не превышает ранга матрицы С. При этом в отличие от обычного метода Лагранжа возможно исключение неизвестных в порядке их нумерации.

                Добавление к матрице жесткости K произведения CTDoC соответствует включению в конструкцию некоторого упругого элемента со специальными свойствами (“нуль-элемента”), который включается параллельно бесконечно жесткой связи и поэтому не искажает результаты расчета. В [17] детально рассмотрены возможные способы конструирования таких “нуль-элементов”, часть из них использована при разработке комплеса SCAD.

Учет особенностей работы конечных элементов

                При создании расчетной схемы необходимо тщательно следить за тем, какие внутренние усилия могут возникать в применяемых конечных элементах и как эти усилия согласуются друг с другом в общих узлах. Так, например, при примыкании стержневого элемента (ригеля) к балке-стенке отсутствует момент в ригеле на опоре (в месте примыкания) при задании вертикальных и горизонтальных нагрузок на ригеле (рис. 20.9.а).

                В качестве общего правила следует считать, что если какое либо усилие (в приведенном выше примере — момент) не воспринимается конечным элементом, то такой элемент по отношению к указанному усилию примыкает к узлу «шарнирно».

                Для учета момента в точке примыкания необходимо запретить угловое перемещение путем наложения соответствующей связи. Это соответствует предположению о том, что изгибная жесткость балки-стенки на несколько порядков превышает изгибную жесткость ригеля. Результаты расчета (рис. 20.9.б) оказываются другими — в месте примыкания ригеля возникает момент.

а) б)

в) Рис. 20.9. Результаты расчета: а - до введения связей; б - после введения связей; в - фрагмент уточненной схемы

               

Конечно, введение защемления моделирует работу системы не очень точно. Более корректным было бы другое изменение расчетной схемы, при котором ригель продлевался бы далее, заходил на балку-стенку на один ряд конечных элементов и крепился не в одном, а в двух узлах (рис. 20.9.в). Такое решение в большей мере соответствует конструкции здания, в которой ригель заводится внутрь стенки для опирания.

Аналогичные приемы используются во всех случаях, когда возникает необходимость рассмотреть сопряжение элементов различной размерности ? стержней (одномерные) с пластинами (двумерными) или объемными (трехмерными) элементами, пластин и оболочек с массивами и т.п. На рис. 20.10 показан пример такого сопряжения, в котором цилиндрическая оболочка стенки и сферическая оболочка крышки защитной конструкции атомного реактора сопрягается с массивным кольцом. Необходимо заметить, что в месте взаимопроникновения конструкций появляется некоторое возмущение жесткостных параметров, которое следует учесть при назначении их величин.

Рис. 20.10. Сопряжение стенки и крышки защитной оболочки реактора с массивным кольцом

Унификация

При вычислении расчетных сочетаний нагрузок предусмотрена возможность унификации в рамках заданных списков (групп) элементов. Реализованы три типа унификации:

в группе элементов сечения унифицируются таким образом, что все элементы группы имеют одинаковое сечение;

в группе элементов выполняется унификация по соответствующим сечениям, т.е. элементы группы будут иметь одинаковые первое, второе, третье и т.д. сечения;

в группе элементов унифицируются симметричные сечения, т.е. все элементы группы будут иметь одинаковые первое и последнее сечения, второе и предпоследнее и т.д.

Для каждого типа унификации может быть задано до девяти групп. Очевидно, что для пластинчатых и оболочечных элементов, а также для элементов включаемых в состав одного физического стержня (конструктивного элемента), может использоваться только первый тип унификации.

Вычисление РСУ в случае унификации выполняется не для каждого элемента в отдельности, а для каждой группы элементов. При этом, в одну группу могут входить только те элементы, у которых одинаковая ориентация местных осей.

Данные для унификации РСУ задают­ся в диалоговом окне Унификация (рис. 11.3). При вводе новых данных рекомендуется:

Ä      нажать кнопку Новый список (элементов);

Ä      выбрать тип унификации из одноименного списка;

Ä      установить номер группы унификации из списка Номер группы;

Ä      ввести список элементов или загрузить созданные ранее группы;

Ä      нажать на кнопку Сохранить.

Для внесения изменений в ранее созданный список или в его характеристики следует:

Ä      в окне Номер списка установить номер модифицируемого списка;

Ä      внести изменения в характеристики списка;

Ä      запомнить изменения, нажав кнопку Сохранить.

                И, наконец, для удаления ранее созданного списка – выбираем этот список и нажимаем кнопку Удалить.

Рис. 11.3. Диалоговое окно

Унификация

Управление нелинейным расчетом

Нелинейные расчеты выполняются с применением шагового метода, идея которого основана на отслеживании поведения системы при относительно малых приращениях нагрузки. При этом на каждом шаге решается линеаризованная система разрешающих уравнений для текущего приращения вектора узловых нагрузок, сформированного для рассматриваемого нагружения.

Расчет ориентирован на решение нелинейных задач в нескольких модификациях шагового метода:

простой шаговый метод ? решает линеаризованную задачу на каждом шаге;

шаговый с уточнениями;

шагово-итерационный.

В первом случае (рис. 18.1.а) на каждом шаге решается линеаризованная задача и в предположении, что это решение является достаточно точным, реализуется переход к следующему шагу нагружения. Погрешность решения нелинейной задачи не контролируется, количество шагов задается пользователем.

Второй вариант предусматривает итерационное уточнение нагружения очередного шага за счет учета невязки в уравнениях равновесия. При этом итерации выполняются с неизменным значением линеаризованной матрицей жесткости (рис. 18.1.б), которая была вычислена в начале очередного шага.

Наконец, в третьем случае производится итерационное уточнение решения на каждом шаге с корректировкой линеаризованной матрицы жесткости на каждой итерации, (рис. 18.1.в).

Шаговый процесс имитирует поведение системы при увеличивающейся (уменьшающейся, при отрицательных значениях коэффициента загружения) интенсивности нагрузок действующих на систему. При этом предполагается, что все компоненты нагрузок, относящиеся к указанному нагружени. увеличиваются (уменьшаются) одновременно в одной и той же пропорции.

Реализована возможность исследования истории нагружения в форме задания последовательности отдельных вариантов нагружения. В этом случае начало приложения нового нагружения соответствует окончанию предыдущего нагружения, т.е. новое загружение является продолжением предыдущего загруже­ния. В частности, возможно использование ранее смоделированного загружения, но с отрицательной величиной коэффициента загружения, что позволяет исследовать полный цикл "нагрузка-разгрузка". Этот прием дает возможность по расхождению начального и конечного состояний системы оценить точность расчета.

Анализ напряженно-деформированного состояния конструкции с учетом нелинейных эффектов выполняется в тех случаях, когда в расчетной схеме задан по крайней мере один нелинейный элемент. В качестве таких элементов могут быть назначены стержни различного вида, трех и четырехузловые элементы оболочек, для которых предусмотрен учет геометрической нелинейности, а также одно и двухузловые элементы, моделирующие односторонние связи (см. главу 4). Допускается комбинирование в одной задаче линейных и нелинейных конечных элементов.

Данные для управления анализом напряженно-деформированного состояния конструк­ции задаются в диалоговом окне Управление шаговым процессом (рис. 18.2), которое вызыва­ется из раздела Специальные исходные данные дерева управления проектом (операция Моделирование нелинейных нагрузок).

Рис. 18.1. Графическая иллюстрация шагового процесса

Диалоговое окно содержит список заданных нелинейных загружений, таблицу для моделирования нагружения конструкции, список для выбора модификации шагового метода, поле ввода количества итераций, а также ряд исполнительных кнопок. В каждой строке таблицы вводятся данные, описывающие один шаг. Для подговки данных следует:

Ä    в столбце Номер загружения выбрать из списка номер линейного загружения;

Ä    в столбце Коэффициент загружения ввести коэффициент к нагрузке для текущего шага в виде множителя к абсолютной величине нагрузки;

Ä    в столбце Количество шагов ввести количество шагов, которые следует выполнить с заданным коэффициентом (если число больше единицы, то шаг будет состоять из нескольких шагов, каждый из которых будет выполняться с заданным в предыдущем столбце коэффициентом загружения);

Ä    в столбце Сохранение результатов активизиро­вать опцию, если предполагается анализ результа­тов текущего шага (если в столбце Количество шагов задано число больше единицы, то  выдается только результирующая информация без резуль­татов промежуточных шагов);



Ä    в списке Метод выбрать необходимую моди­фи­кацию шагового метода;

Ä    если выбран шагово-итерационный метод, то в поле Количество итераций ввести максимальное число итераций;

Ä    повторить перечисленные выше действия для каждого шага анализа;

Ä    нажать на кнопку Записать, после чего подготовленные данные попадут в список нелинейных загружений;

Ä    если необходимо подготовить несколько списков, то нажать кнопку Новый список и повторить перечисленные действия для других загружений;

Ä    в тех случаях, когда результаты расчета нового списка являются продолжением нагружения предыдущего, то после нажатия кнопки Новый список

следует активизировать опцию Загружение является продолжением предыдущего загруже­ния.

                Для удаления текущего списка используется кнопка Удалить список. Если нажать кнопку Удалить данные, то удаляется вся управляющая информация и выполнение нелинейного расчета блокируется.



Рис. 18.2. Диалоговое окно

Управление шаговым процессом

«От расчетчика – пользователя программными комплексами, интересующегося напряженно-деформированным состоянием, не требуется детального знания всех математических, вычислительных и компьютерных проблем. Однако ему необходимо иметь представление о том, как математически формулируются задачи и что представляют собой численные методы их решения. Без этого трудно рационально выбрать расчетную схему и правильно оценить достоверность окончательных результатов.»

Л.А. Розин Задачи теории упругости и численные методы их решения. –  Санкт-Петербург: СПбГТУ, 1998, стр.5

Управление выводом исходных данных

Работа в окне Исходные данные

(рис.9.2.5) заключается в назначении данных, которые выводятся на печать. Данные разделены на две группы. С помощью кнопок, расположенных в верхней части окна, назначаются виды таблиц с информацией о различных характеристиках расчетной схемы. Расположенные справа кнопки служат для вывода на печать управляющей информации. В нижней части окна расположено поле для ввода комментариев к исходным данным.

Рис. 9.2.5. Диалоговое окно

    Исходные данные

Для предварительного просмотра таблиц используется кнопка Просмотр в окне Вывод результатов. После нажатия этой кнопки происходит формирование таблиц с учетом всех выполненных настроек, заданного вида и размера шрифта, иллюстраций и комментариев. Полученные таблицы отображаются в окне (рис. 9.2.6). Листание возможно только в сторону увеличения номеров страниц. При необходимости можно вывести на печать содержание текущей страницы, используя кнопку

.

Просмотр таблиц

Рис. 9.2.6. Окно режима просмотра таблиц

Условия сопряжения элементов с узлами системы

                Примыкающие к узлам системы узлы (концевые сечения) элементов, вообще говоря, могут геометрически располагаться на некотором отдалении от центра узла схемы, т.е. может иметь место некоторый эксцентриситет примыкания. Будем считать, что для тех типов элементов, где такой эксцентриситет допустим, узел (концевое сечение) элемента соединен с центром узла схемы бесконечно жесткой вставкой и эта вставка является частью конечного элемента (см. описание конечных элементов стержневого типа в главе 3).

                Естественно, что при наличии упомянутой бесконечно жесткой вставки перемещение концевого сечения элемента не равно перемещению узла схемы (оно зависит также и от узловых поворотов), а углы поворота узла и концевого сечения совпадают.

                Несовпадение перемещений (поворотов) узла и связанной с узлом схемы концевого сечения элемента может иметь место и в силу особенностей конструкции примыкания. Если считать, что элементы могут быть прикреплены своими узлами к центрам узлов схемы с помощью шести связей, каждая из которых препятствует одному из шести их возможных взаимных перемещений, то можно себе представить и отсутствие любой из этих шести связей. Отсутствие одной связи между угловыми перемещениями соответствует цилиндрическому шарниру, отсутствие трех связей для всех взаимных угловых перемещений – сферическому шарниру, отсутствие связи и между линейными смещениями – “ползуну” и т.п. Для краткости дальше все такие случаи называются “шарнирами”, хотя тут имеется и определенная неточность. Здесь необходимо отметить, что использование различных типов соединения элементов с узлами и связей, накладываемых на узловые перемещения, позволяет разнообразить описание расчетной схемы, что иллюстрируется и рисунком 19.1. На этом рисунке рекомендуем сравнить равноценные, но по-разному представленные пары узлов 1 и 4 или 7 и 8.

                Следует заметить, что возможность введения неполного совпадения перемещений узла элемента и узла схемы, равно как и возможность эксцентричного примыкания, предусмотрена не для всех типов элементов и здесь следует руководствоваться соответствующими указаниями из описания конечных элементов. Обход имеющихся запретов возможен с использованием искусственных приемов (введение дополнительных узлов, весьма податливых элементов – связей и др.).

Установка номера загружения

Номер загружения или комбинации нагрузок выбирается из списка (рис. 7.1.3) Выбор номера загружения, установленного в разделах Деформации, Эпюры усилий и Поля напряжений. Перед номером загружения стоит буква L, а номером комбинации нагрузок – С. Если загружение динамическое, то его номер комбинируется из номеров загружения и формы. Перед номером формы стоит буква М. В разделе Деформации

предусмотрена возможность анализа перемещений в узлах конструкции под действием сил, соответствующих формам собственных колебаний. В этом случае номер загружения и форма идентифицируются буквой М (например, L3 – М5). 

Установленный в одном из разделов номер загружения действует для всех остальных разделов. В тех случаях, когда при создании загружений им были присвоены имена, они следуют в списке за номером загружения.

 Рис. 7.1.3. Список выбора номера загружения

Устойчивость

Для каждого указанного пользователем загружения (или комбинации загружений) SCAD позволяет определить:

коэффициент запаса устойчивости;

первую форму потери устойчивости (без анализа кратности);

свободные длины стержневых элементов.

13.1 Постановка задачи

Задача устойчивости решается в классической постановке для упругой системы и в предположении, что все приложенные к системе внешние нагрузки (следовательно, и внутренние силы) растут пропорционально одному и тому же параметру l. То значение параметра l, при котором матрица жесткости системы А(l) впервые  перестает быть положи­тельно определенной, является критическим, а соответ­ствующее значение l — коэффициентом запаса устойчивости (КЗУ). Матрица жесткости А(l) = Ao

- B(l) состоит из “обычной” матрицы жесткости Ao и матрицы “толкающих” реакций B(l), которые определяются сжимающими силами в стержнях, напряжениями сжатия в конечных элементах оболо­чечного типа и т.п. Напоминаем, что положительная опреде­лен­ность матрицы жесткости означает, что при любых значениях узловых перемещений и поворотов u потенциальная энергия системы положительна (это значит, что для деформирования системы необходимо затратить энергию и, следовательно, она оказывает сопротивление деформированию, она является отпорной).

                Если система теряет устойчивость, она теряет отпорность и ее матрица жесткости становится вырожденной (с нулевым детерминантом), а в закритическом состоянии система получает отрицательную отпорность (при ее принуди­тельном деформировании выделяется ранее накопленная потенциальная энергия “толкающих” реакций) и ее матрица жесткости становится знаконеопределенной.

                Таким образом, задача оценки устойчивости равно­весия сводится к проверке положительной определен­ности матрицы жесткости при пробном значении коэффициента l.

                Необходимо отметить, что с помощью проверок матрицы жесткости можно отыскать только те критические состояния, при которых потеря устойчивости происходит по форме, когда узловые перемещения и повороты не все вместе равны нулю (это так называемая явная форма потери устойчивости). Нужно еще проверить, что при пробном значении l не может произойти так называемая скрытая форма потери устойчивости, которая реализуется в пределах одного конечного элемента и не вызывает узловых перемещений и поворотов. Поскольку для всех типов конечных элементов соответствующие критические величины lкр известны (они вычисляются по простым формулам), то это значит, что следует, кроме всего прочего, проверить неравенство l > lкр для всех конечных элементов.

13.2 Поиск коэффициента запаса устойчивости

Поиск коэффициента запаса устойчивости (КЗУ) ведется в интервале [0,L], где L ? число, заданное пользователем, ( оценка того значения КЗУ, которое считается уже безразличным для оценки качества системы) и с точностью e, которая также задается пользователем.

                При этом решается задача определения минимального l, при котором происходит вырождение матрицы А(l).

                Матрица А(l) составляется из матриц устойчивости отдельных конечных элементов. Если в системе нет ни одного элемента, способного терять устойчивость (например, в стержневой системе все стержни растянуты), то выдается сообщение, что система "абсолютно устойчива".

                Далее проверяется устойчивость системы при l = L (т.е. положительная определенность матрицы А(L)). Если это условие выполнено, то выдается сообщение о том, что КЗУ больше заданного максимума.

                Если условие положительной определенности А(L) не выполнено (об этом свидетельствуют отрицательные значения на главной диагонали матрицы жесткости, преобразованной в процессе решения системы уравнений), производится анализ положительной определенности матрицы А(L/2),..., т.е. используется стандартный метод половинного деления. Этот процесс продолжается до тех пор, пока не найден интервал (l1, l2) такой, что l2 - l1 £ e и матрица А(l1) положительно определена, а матрица А(l2) этим свойством не обладает. При этом величина l1

считается КЗУ.

                При составлении матрицы устойчивости для каждого конечного элемента (способного терять устойчивость) вычисляется значение lкр, которое приводит к потере устойчивости КЭ. Если min lкр

< L, интервал поиска сокращается, а номер элемента, для которого достигается min lкр, сообщается в протоколе.

13.3 Форма потери устойчивости

В предположении, что определенный на первом этапе коэффициент запаса устойчивости является точным, SCAD производит решение задачи об определении собственного вектора при известном собственном значении задачи



                (A - B(l1)) u = 0.                                   (а)

                Заметим, что правые части системы равны нулю, т.е. отыскиваются такие значения узловых перемещений и пово­ротов u, которые вызываются только внутренними сжимающи­ми напряжениями и усилиями. Поперечные нагрузки, как известно, не влияют на значения критических сил и вид формы потери устойчивости. Поскольку уравнение (а) решено при нулевой правой части, то форма потери устойчивости определена лишь с точностью до множителя. Ее уменьшение или увеличение в любое число раз не нарушает условие (а).

13.4 Свободные длины

Если в системе имеются стержневые элементы, то можно определить их свободные длины, т.е. длины таких же, но шарнирно опертых стержней, у которых критическая сила Nкр совпадает с продольным усилием в стержне системы в момент потери устойчивости (Nкр=l1*N). Поскольку по формуле Эйлера   Nкр = p2EJ / l2, свободная длина будет lo = (l1N

/  p2EJ )1/2,

где EJ ? жесткости стержней в главных плоскостях инер­ции (для пространственной задачи ? по две для каждого стержня).

13.5 Ввод данных

               

Ввод данных для проверки устойчивости выполняется в одноименном диалоговом окне (рис. 13.5.1), которое вызывается из раздела Специальные исходные данные в Дереве проекта. Для ввода данных необходимо выполнить такие операции:

Ä      с помощью комбинаторных кнопок задать режим проверки ? вычисление коэффициента запаса устойчи­вости, форм потери устойчивости и свободных длин стержневых элементов;

Ä      в полях Масштабный множитель и Точность вычислений

следует ввести соответствующие значения (по умолчанию приняты 2 и 0.01);

Ä      активизировать опции, определяющие вид данных, для которых выполняется проверка устойчивости: по загруже­ниям или по комбинациям загружений, для всех загружени­й (комбинаций) или только для выбранных; в послед­нем случае выбор нужных данных выполняется в списке загружений (комбинаций).

Масштабный множитель ? параметр используется для ограничения интервала поиска коэффициента запаса устойчивости. Если его значение больше заданного, система считается устойчивой.

Точность вычислений - параметр задает критерий окончания итерационного процесса поиска коэффициента запаса устойчивости. При очень малых значениях этого параметра время расчета может существенно увеличиться.

                Для удаления подготовленных данных и отказа от анализа устойчивости используется кнопка Удаление данных.



Рис. 13.5.1. Диалоговое окно

Проверка устойчивости

Ветровая нагрузка

                В основу методики положен подход из раздела 10 справочника [5], где задача о действии турбулентных пульсаций ветрового потока поставлена как задача статистической динамики.

                Давление ветра на сооружение в точке, расположенной на высоте z от уровня земли, рассматривается как сумма статической и пульсационной составляющих ветровой нагрузки

                                                                      q(z,t) = qs(z) + qp(z,t).                                                                                        (19.27)

                Последняя есть случайная функция времени, обусловленная случайной скоростью пульсаций, имеющей нулевое среднее, стандарт s(z) и безразмерный спектр Давенпорта

                                                              S(e) = 1200e5/3 /[3vo(1 + e2)4/3],                                                                                (19.28)

где vo – среднечасовая скорость ветра на высоте 10м; e = vo/1200q – безразмерный период колебаний.

                С учетом упрощений, достигаемых за счет предположения о полной коррелированности (пульсации скорости ветра рассматриваются как синхронные по пространству случайных функций только времени) среднеквадратичное смещение по j-ой компоненте вектора Z представляется в виде

                                                                     Zä.j =

(h2ijm2i)/w4i .                                                                                                                                   (19.29)

Здесь s – число учитываемых форм собственных колебаний, hij – приведенное ускорение, вычисляемое по формуле

                                                            hij = (Yij

Yik)/

Yir ,                                                                                                                      (19.30)

а квадрат коэффициента динамичности определяется так:

                                       m2 = (2/3)

(1 + e2)-4/3

[e4 - 2(1 - g2/2)e2e2i

+ e4i]-1 de.яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.31)

яяяяяяяяяяяяяяя Џ а ¬Ґва § вге ­Ёп g бўп§ ­ б «®Ј аЁд¬ЁзҐбЄЁ¬ ¤ҐЄаҐ¬Ґ­в®¬ d § ўЁбЁ¬®бвмо g = d/p,   зҐаҐ§ eiя ®Ў®§­ зҐ­ ЎҐ§а §¬Ґа­л© ЇҐаЁ®¤ б®Ўб⢥­­ле Є®«ҐЎ ­Ё© ei = vo/1200q.

яяяяяяяяяяяяяяя ђ бзҐв­лҐ бв вЁзҐбЄЁҐ ЇҐаҐ¬ҐйҐ­Ёп бўп§ ­л б ЇҐаўл¬ б« Ј Ґ¬л¬ ў (19.27),   ¤Ё­ ¬ЁзҐбЄЁҐ -®ЇаҐ¤Ґ«повбп Ї® д®а¬г«Ґ (19.29). “бЁ«Ёп ў н«Ґ¬Ґ­в е бЁбвҐ¬л Ё ЇҐаҐ¬ҐйҐ­Ёп ҐҐ в®зҐЄ (®Ў®ЎйҐ­­® - ®вЄ«ЁЄ б®®а㦥­Ёп •) ­ е®¤пвбп а §¤Ґ«м­® ®в бв вЁзҐбЄ®© б®бв ў«по饩 ўҐва®ў®© ­ Јаг§ЄЁ Ё ®в Ё­ҐажЁ®­­ле бЁ«, ᮮ⢥вбвўгойЁе Є ¦¤®© д®а¬Ґ б®Ўб⢥­­ле Є®«ҐЎ ­Ё©. ‘㬬 а­®Ґ §­ зҐ­ЁҐ ®вЄ«ЁЄ  ®ЇаҐ¤Ґ«пҐвбп Ї® д®а¬г«Ґ

яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя X = Xc + []1/2,яяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяяя (19.32)

Ё§ Є®в®а®© ўЁ¤­®, зв® Є®«ҐЎ ­Ёп б®ўҐаи овбп ў®Єа㣠ᬥ饭­®Ј® б®бв®п­Ёп а ў­®ўҐбЁп, ᮮ⢥вбвўго饣® бв вЁзҐбЄ®© (б।­Ґ©) Є®¬Ї®­Ґ­вҐ ­ Ја㦥­Ёп. Љ®¬Ї«ҐЄб ўл¤ Ґв ®в¤Ґ«м­лҐ б®бв ў«пойЁҐ ¤Ё­ ¬ЁзҐбЄ®Ј® ®вЄ«ЁЄ  яЁ б㬬 а­®Ґ §­ зҐ­ЁҐ (19.32), ЇаЁзҐ¬ §­ Є ЇҐаҐ¤ ўв®ал¬ б« Ј Ґ¬л¬ ЇаЁ­Ё¬ Ґвбп в ЄЁ¬ ¦Ґ, Є Є Ё г Є®¬Ї®­Ґ­вля Xc.

Внешние и внутренние связи

                В силу особенностей конструктивного решения на некоторые из узловых перемещений могут быть наложены ограничения (связи). Говорят, что на систему наложена моносвязь, если она запрещает одну из компонент узлового перемещения (например X=0 или UY=0). Если же в силу наложенной на систему связи аннулируется некоторая линейная комбинация компонент узловых перемещений, то говорят о полисвязи [17]. Моносвязь всегда является внешней связью, поскольку она как бы извне системы ограничивает ее перемещения. Полисвязь, наложенная на компоненты узловых перемещений одного и того же узла, также является внешней, только направление запрещенного перемещения не совпадает с осями координат, а ориентировано под некоторым углом (например, полисвязь Xicosj + Yisinj=0 ориентирована под углом j к координатной оси X). Другие полисвязи, где фигурируют компоненты перемещений различных углов, являются внутренними и чаще всего обусловлены наличием в системе (в ее расчетной схеме) абсолютно жестких элементов.

                Необходимо отметить, что при выборе расчетной схемы следует опасаться того, чтобы бесконечно жесткие элементы, моделирующие внутренние связи, не образовали статически неопределимую систему, например, замкнутый контур. Система тогда становится вырожденной, а усилия в ней распределяются не единственным способом.

                Другой, в некотором смысле противоположной, опасностью при создании расчетной схемы является пропуск связи, т.е. отсутствие запрета на перемещение, приводящее к появлению геометрической изменяемости. Эта ошибка может быть скорректирована и автоматически, однако пользователь всегда должен помнить о том, что это есть следствие его недосмотра и внимательно оценить “услугу” системы по исправлению обнаруженной ошибки. В частности, такая корректировка справедлива лишь тогда, когда реакции в автоматически установленных дополнительных связях равны нулю и по направлению данного смещения не действует нагрузка.

                Расчет системы, на которую наложены моносвязи, достаточно прост – соответствующие узловые перемещения исключаются из числа основных неизвестных. В связи с этой простотой возникает естественное стремление описать в виде моносвязей и те внешние связи, которые запрещают перемещения или повороты, не ориентированные вдоль координатных осей.

                Можно попытаться запретить любое перемещение и путем установки некоторых дополнительных элементов, придав им достаточно большую жесткость, однако такой прием является приближенным и может привести к существенной потере точности, хотя и имеет то преимущество, что позволяет определить реакцию введенной связи. Более широкие возможности предоставляет использование специальных “нуль-элементов”, которые, кроме всего прочего, позволяют выполнить расчет на заданное смещение [17].

Водонасыщенные грунты

Во многих случаях, в особенности при рассмотрении гидроэнергетических сооружений, следует считаться с тем, что грунты основания являются водонасыщенными. Теория таких сред, развитая Био [22], в которой учитывается упругое и вязкое взаимодействие твердой и жидкой фаз в пористоупругой насыщенной жидкостью двухфазной среде, достаточно сложна и используется чаще всего при решении весьма специфических проблем. Однако, можно рассмотреть предельные случаи водонасыщенной среды, различаемые по степени связности между твердой и жидкой фазами грунта.

Первым предельным случаем является среда "без связи", в которой жидкость свободно циркулирует между зернами твердой фазы (маловлажные пески, песчаники). Второй предельный случай ? "совершенная связь", характеризуется тем, что жидкость не может циркулировать в замкнутых порах (глины, известняки) и выдавливается из них при действии внутренних напряжений.

Критерием для оценки перехода к предельным случаям является значение безразмерной константы

                                                                

                                                                                   (20.15)

где m ? пористость, rf и rs ? плотность жидкой и твердой фаз, A ? полуширина фундамента, KF

? коэффициент фильтрации, C2 ? скорость распространения поперечной волны, g ? ускорение свободного падения. Константа В в среде без связи стремится к нулю, а в среде с совершенной связью ? к бесконечности. При этом основными характеристиками, определяющими значение В, являются скорости распространения продольной и поперечной волн V1 и V2, а также коэффициент Пуассона.

                Для среды без связи скорости распространения волн вычисляются по формулам

                                          

                                                             (20.16)

где l и m — параметры Ляме.

                Для среды с совершенной связью

                                                (20.17)

Здесь Ks и Kf — истинные модули сжимаемости твердой и жидкой фаз.

                Расчеты для указанных предельных случаев выполняются как для упругой среды со следующими значениями определяющих упругих параметров:

коэффициент Пуассона n = (1 - 2b2)/(2 - 2b2), где b = С2/С1;

модуль упругости Е = 2m(1 + n).

                Необходимо отметить, что константа В зависит от размера фундамента, и при одних и тех же грунтах использование той или иной расчетной модели будет также зависеть от полуширины фундамента А. Так, например, для водонасыщенного песка с характеристиками l = 0,23´109

Н/м2; m = 0,1´109 Н/м2; Ks = 3,6´1010

Н/м2; Kf = 1,92´109 Н/м2; m = 0,45; rs = 2,65´103

Н/м3; rf = 1,0´103

Н/м3; КФ = 10-2 м/с критериальная константа В = 0,52А. Следовательно, при малых размерах фундамента В Þ 0 (или, точнее, В << 1) и можно пользоваться моделью "среды без связи" с характеристиками n = 0,35 и Е = 2,7´108

Н/м2.

20.5. Использование абсолютно жестких вставок

При расчете стержневых систем часто возникает необходимость учесть эксцентричность стыковки элементов в узлах (рис. 20.14.а).



Рис. 20.14. Ступенчатый  стык

Вставка между узлами n и n+1 стержня с очень большой, но конечной жесткостью, как это представляется интуитивно возможным, приводит к резкой потере точности вычислений за счет ухудшения числа обусловленности матрицы жесткостей [29]. Для обхода этой вычислительной трудности в комплексе SCAD предусматривается возможность использовать бесконечно жесткие вставки по концам стержневых элементов. Тогда расчетная схема имеет только один узел, занимающий произвольное положение на прямой между узлом n и узлом n+1, и к этому узлу концевые сечения соседних элементов присоединяются через жесткие вставки. Потеря точности в этом случае не наблюдается[1]. Проще всего можно поступить, если единственный узел N совместить с одним из узлов пары n, n+1, тогда абсолютно жесткая вставка появиться только у одного из элементов.

                Платой за это упрощение является то, что внутренние усилия будут определены лишь на упругой части стержня.



                Использование абсолютно жестких вставок особенно рекомендуется в тех случаях, когда рассматривается плита или оболочка, подкрепленная ребрами, эксцентрично расположенными по отношению к срединной поверхности. Если эти ребра моделируются стержневыми элементами, то учесть эксцентриситет можно лишь при использовании абсолютно жестких вставок.



Рис. 20.15.

При расчете стержневых систем высота сечения обычно не превышает 1/8 ¸ 1/10 расстояния между узлами. Но встречаются конструкции, когда это отношение доходит до 1/5  или даже 1/3 (некоторые виды фундаментов под турбоагрегаты, диафрагмы зданий, гидротехнические сооружения и др.). В этом случае стержневая расчетная схема с точечными узлами, расположенными на пересечениях осей элементов, становится некорректной. Широко распространено предложение учитывать при этом реальные размеры "узлов", используя для этих целей стержневые элементы с бесконечно жесткими вставками. Пример такой схемы, построенный в соответствии с рекомендациями [32], представлен на рис. 20.15. Этот прием настолько давно используется, что расчеnчики практически никогда не задают вопрос о правомерности использования гипотезы недефомируемости "узла". Вместе с тем он далеко не лишен смысла, что видно из рассмотрения результатов расчета модельной задачи (рис.20.16)

Рис. 20.16. К анализу работы узла конечных размеров

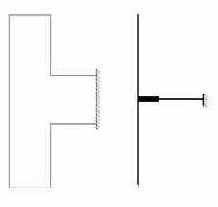В ее стержневой модели горизонтальные перемещения отсутствуют, и вертикальный стержень не изгибается. Более детальная расчетная схема указывает на наличие горизонтальных перемещений, которые возникают вследствия стеснения деформаций сжатия по линии сопряжения АБ. Поскольку на противоположной стороне "стойки" этого стеснения нет, то возникает неравномерность распределения напряжений, эквивалентная изгибу.

20.6. Расчет на заданные перемещения

                Необходимость расчета на заданные смещения возникает в практике проектирования чаще всего тогда, когда рассматриваемая система прикреплена к другой намного более мощной системе, которая не входит в расчтеную модель и играет роль "земли". Если упомянутая мощная система испытывает некоторые деформации, то для рассчитываемой конструкции следует учесть навязываемые смещения опорных узлов. Необходимо обязательно отметить, что могут задаваться лишь те перемещения узла, которые в отсутствие деформационного равны нулю (неподвижны), т.е. этот тип нагружения определяется перемещениями связей.



                Для расчета на заданные смещения связей в SCAD предусмотрено использование нуль-элементов [17], схема простейшего элемента такого типа представлена на рис. 20.17. Он представляет собой комбинацию последовательно соединенных друг с другом пружин положительной жесткости С

и отрицательной жесткости -С. Поскольку для последовательно соединенных элементов податливости 1/С и 1/(-С) суммируются, то полученный элемент суммарной нулевой податливости по отношению к взаимному смещению его крайних узлов является абсолютно жесткой связью.

                Если в качестве внешнего воздействия на систему необходимо приложить принудительное смещение пары внешних узлов на величину D, то достаточно приложить к внутреннему узлу нуль-элемента силу силу Р = СD и уравновесить ее в другом узле (см. рис. 20.17.б).



Рис. 20.17. Нуль-элемент

                Все приведенные выше рассуждения остаются справедливыми при любом ненулевом значении параметра жесткости С, но исходя из соображений хорошей обусловленности матрицы жесткостей системы рекомендуется выбирать его не слишком отличающимся от жесткостных параметров близлежащих элементов.

20.7. Скрытые жесткости

Сочетание в одной расчетной схеме элементов (стержней), базирующихся на различных теориях, требует особо внимательного отношения расчетчика к формированию расчетной схемы конструкции. Комплексные механические модели подобного рода могут провоцировать получение некорректных результатов расчета.

В качестве иллюстрации высказанного положения рассмотрим следующую простую по своей постановке задачу. Пусть требуется произвести расчет однопролетной многоэтажной (20 этажей) рамы (так называемой “этажерки”), изображенной  на рис. 20.18.



Рис. 20.18. Схема с двумя типами стержней

Пусть более мощная стойка рамы (стойка “1” на рис.20.18) имеет  характеристики, в отношении которых расчетчик принимает решение о необходимости учета деформаций сдвига. Иначе говоря, для стойки “1” в расчетной схеме используется теория Тимошенко для изгибаемого стержня. Пусть далее в отношении стойки “2” принимается решение об использовании классической теории изгиба стержней, то есть теории Бернулли-Эйлера, основанной на гипотезе плоских сечений при пренебрежении деформаций сдвига. Что касается шарнирно присоединенных к стойкам ригелей, то будем считать их недеформируемыми в продольном направлении, то есть абсолютно жесткими на растяжение - сжатие.



Расчет, изображенной на рис. 20.18 рамы не представляет каких-либо затруднений и может быть выполнен по любой из имеющихся в распоряжении инженера-расчетчика программных систем, способных обрабатывать как стержни Тимошенко, так и классические стержни Бернулли-Эйлера. Возьмем для примера следующие (условные и заданные в условных единицах измерения) жесткостные характеристики, а именно положим:

EI1

= 3,5·109 ,             GF1 = 16,0·106 ,                EI2

= 3,5·107 .

Естественно ожидать, что основная часть нагрузки будет восприниматься более мощной стойкой, то есть стойкой “1”, так как ее изгибная жесткость EI1 на два порядка превышает аналогичную жесткость EI2 стойки “2”. Однако результаты выполненного расчета неожиданно (на первый взгляд) показывают, что значение поперечной силы в нижнем сечении стойки “1” равняется Q1(0) = 0,275Р, тогда как на стойку “2” передается вся оставшаяся часть нагрузки, то есть Q2(0) =  0,725P. Подобное распределение поперечных сил противоречит привычной инженерной интуиции, ожидающей как раз противоположного результата.

Для того чтобы понять причины происхождения этого эффекта, следует учесть, что за условием пренебрежения деформаций сдвига для стерженя Бернулли-Эйлера кроется предположение о его бесконечной жесткости на сдвиг, в то время как для стержня Тимошенко она имеет вполне определенную конечную величину. Именно эта скрытая бесконечная жесткость и определяет перераспределение усилий в системе.

20.8. Учет несовершенств системы

                Расчет, выполняемый с помощью SCAD, основывается на использовании идеализированной расчетной модели, которая, вообще говоря, не учитывает возможные неидеальности. К сожалению, отечественные нормативные документы не уделяют этой проблеме должного внимания. Поэтому приведенные ниже рекомендации базируются на зарубежном опыте, который представлен в Еврокоде-3 (см. ENV 1993-1-1. Design of steel structures. - part 1 "General rules and rules for building").

                Еврокод регламентирует некоторые элементы общего статического расчета несущей системы, допуская определение внутренних сил и моментов методами:



                упругого расчета - для любых систем;

                упруго-пластического или жестко-пластического расчета ? для систем с необходимым подкреплением против потери устойчивости.

                Упругий расчет по недеформированной схеме допускается в тех случаях, когда приращения внутренних сил и моментов DR, возникающие за счет учета влияния перемещений системы под нагрузкой, не превышает 10% от величины R, полученной без учета этого влияния. В частности, для ортогональных многоэтажных рам расчет по недеформированной схеме возможен если

   (d/h) £ 0,1(SH/SV),

где: d ? горизонтальное смещение верха рамы, h ? общая высота конструкции,

 SH ? сумма горизонтальных реакций, SV ? общая вертикальная сила, действующая на раму.

                Возможные несовершенства реальной системы могут привести к снижению уровня критической нагрузки (по сравнению с результатами расчета идеализированной системы). В связи с этим не рекомендуется применять конструкции, у которых коэффициент запаса по общей устойчивости меньше 1,25.

                В отличие от СНиП, EUROCODE требует учета возможных начальных несовершенств и при выполнении общего статического расчета системы. В общем случае учету подлежат несовершенства системы в целом, несовершенства (неидеальность) узловых соединений и несовершенства элементов конструкции.

Для многоэтажных рам таким несовершенством является отклонение от вертикали

Y = kcksYo,

где:         Yo ? допускаемый перекос колонны (например, Yo = 1/200);

                kc = (0,5 + 1/nc)1/2, но kc £ 1;

                ks = (0,2 + 1/ns)1/2, но ks £ 1;

                ns ? число этажей;

                nc ? общее число колонн, проходящих через все этажи, у которых нагрузка не ниже 50% от средней нагрузки на колонну.

                Допускается учитывать эти отклонения в виде эквивалентных горизонтальных сил по схеме рис.20.19. Такие силы могут действовать по всем возможным горизонтальным направлениям и необходимо выбрать неблагоприятные из них (например, для схемы по рис. 20.19, если ветер на раму действует слева направо, то неблагоприятным будет направление сил  yF1



и yF2 ? тоже слева направо).

Рис. 20.19. Эквивалентные силы для учета отклонений от вертикали

Рис. 20.20. Эквивалентные силы для связевых систем

                При расчете связевых систем, обеспечивающих боковую жесткость конструкции, необходимо учитывать начальные несовершенства раскрепляемых элементов в виде их искривлений со стрелкой eo = krL/500, где  kr

= (0,2 + 1/nr)1/2, но kr  £ 1; nr - число подкрепляемых элементов.

                Эквивалентная нагрузка на связевую систему

q = (SN/L)(kr + 500dq/L)/62,5,

где dq ? прогиб связевой системы (рис.20.20).  В тех случаях, когда связевая система стабилизирует изгибаемые элементы, усилия  N могут быть определены как

N = M/h,

где M ? максимальный изгибающий момент и h ? высота изгибаемого элемента.

 

 

 

 

 

 

 

 

 

 

Литература к главам 19 и 20

1.     Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика: Логика и особенности приложений математики. -– М.: Наука, 1983. –328 ñс.

2.     Власов В.З., Леонтьев Н.Н. Балки, плиты, оболочки на упругом основании. —–

М.: Гос.изд. физ.-мат.лит., 1960.

3.     Вовкушевский А.В., Шойхет Б.А. Расчет массивных гидротехнических сооружений с учетом раскрытия швов. —– М.: Энергия, 1981. – —136 с.

4.     Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений.-– ÌМ.: ÌèðМир, 1984.-–

333 ñс.

5.     Динамический расчет зданий и сооружений (Справочник проектировщика) /Под ред. Б.Г.Коренева и И.М.Рабиновича. -– М.: Стройиздат, 1984.- – 303с.

6.     Динамический расчет сооружений на специальные воздействия (Справочник проектировщика)

/Под ред. Б.Г.Коренева и И.М.Рабиновича. -– М.: Стройиздат, 1981. -– 215с.

7.     Доннелл Л.Г. Балки, пластины и оболочки. М.: Гл. ред. ф.-м. наук, 1982. – 568 ñс.



8.     Евзеров И.Д. Оценки погрешности несовместных конечных элементов плиты. Деп. в УкрНИИНТИ, №1467. –— Киев, 1979. –—

9 с.

9.     Елсукова К.П., Сливкер В.И. Некоторые особенности МКЭ при расчете конструкций на упругом основании.

–— В кн. Метод конечных элементов и строительная механика. Труды ЛПИБ №349. —– с.69-80.

10. Зенкевич О. Метод конечных элементов в технике. –— М.: Мир, 1975. —– 542 c.

11. Зенкевич О., Морган К. Конечные элементы и аппроксимации. МÌ.: ÌèðМир, 1986. –

318 ñс.

12. Зенкевич О.К., Айронс Б.М., Скотт Ф.К., Кемпбелл Дж. С. Анализ трехмерного напряженного состояния. —–  В кн.: Расчет упругих конструкций с использованием ЭВМ. Том 1. —–

Л.: Судостроение, 1974, с. 293-305.

13. Карпиловский В.С. Методы конструирования конечных элементов. Деп. в УкрНИИНТИ, №3153.— –

Киев, 1980.

–— 20 с.

14. Метод суперэлементов в расчете инженерных сооружений. /В.А.Постнов, С.А.Дмитриев, Б.К.Емышев, А.А.Родионов. –- Л.: Судостроение, 1989. -– 288с.

15. Методы расчета стержневых систем, пластин и оболочек с использованием ЭВМ.  ÷àñòüЧасть

11. / Под ред. Смимрнова А.Ф./ М.: Стройиздат, 1976. – 248 с.

16. Пастернак П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. – М. – Л.: Гос. изд. лит. по строительству и архитектуре, 1954.

17. Перельмутер А.В., Сливкер В.И. О реализации сложных кинематических условий при расчете дискретных систем методом перемещений. – В кн.: Метод конечных элементов и строительная механика. Труды ЛПИ N 369. Л 1979. С.26-39.

18. Пискунов В.Г., Карпиловский В.С. и др. Расчет кpановыx констpукций методом конечныx элементов. М.: Машиностроение, 1991. – 240 с.

19. Пискунов В.Г., Федоренко Ю.М. Динамический метод контроля состояния слоистых плит на упругом основании, Архитектура и строительство Белоруси, №5-6, 1994, с.19-22

20. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Гл. ред. ф.-м. наук,1988. – 712 с.



21. Ржаницын А.Р. Устойчивость равновесия упругих систем. М.: Гостехстройиздат, 1955. – 475 с.

22. Сеймов В.М., Трофимчук А.Н., Савицкий О.А. Колебания и волны в слоистых средах. – Киев: Наукова думка, 1990.

23. Смирнов А.Ф., Александров А.В., и др. Строительная механика. Стержневые системы. М.: Стройиздат, 1981. – 512 с.

24. СНиП II-7-81. Строительство в сейсмических районах / Госстрой СССР. – М.:Стройиздат, 1982. – 48 с.

25. Стрелец-Стрелецкий Е.Б. Расчетные сочетания напряжений для конструкций типа балки-стенки и плиты. Строительная механика и расчет сооружений. 1986. N3.

26. Стренг Г., Фикс Дж. Теория метода конечных элементов. – М.: Мир, 1977. – 350 с.

27. Сьярле Ф. Метод конечных элементов для эллиптических задач. М.: Мир, 1980. – 512 с.

28. Феодосьев В.И. Десять лекций-бесед по сопротивлению материалов. – М.: Наука, 1969.

29. Чу К.-С. Определенный вид плохо обусловленной матрицы жесткостей, Ракетная техника и космонавтика, 1973, №1, с.125-127.

30. Sabahi D., Rose T. Special Applications of Global-Local Analysis, MSC/NASTRAN 1992 World Users` Conference Proceedings.

31. Schiermeier J.E., Housner J.M., Ranson J.B., Aminpour M.A., Stroud W.J. The Application of Interface Element to Dissimilar Meshes in Global/Local Analysis, MSC 1996 World Users` Conference Proceedings

32. Городецкий А.С., Евзеров И.Д., Стрелец-Стрелецкий Е.Б., Боговис В.Е., Гензерский Ю.В., Городецкий Д.А. Метод конечных элементов: теория и численная реализация. Программный комплекс "Лира-Windows". – К.: ФАКТ, 1997.

Выбор анализируемого фактора

Рис. 7.1.4. Список выбора направлений перемещений

Анализируемый фактор выбирается из списка, установленного в разделах Деформации, Эпюры усилий, Поля напряжений и Постпроцессоры (рис. 7.1.4). Если выбор осуществляется в рамках одной группы факторов, например, перемещений, отображение фактора выполняется сразу. Смена номера загружения или вида анализируемой информации требует определенного времени, которое существенно зависит от размерности задачи.

Следует отметить, что условия работы конструкции могут привести к нулевым значениям некоторых факторов. Например, для плоской ферменной системы отсутствует перемещение по направлению оси Y.

Вывод изолиний и изополей

                Для пластинчатых и объемных элементов пере­мещения и силовые факторы могут выводиться в виде изоли­ний или изополей. Кроме того силовые факторы могут отобра­жаться цветовыми маркерами в центрах элементов. Выбор вида отображения выполняется кнопками, установ­ленными в соответствующих разделах инструменталь­ной панели:

 – вывод изолиний;

 – вывод изополей;

 – вывод изополей и изолиний;

 – отображение напряжений цветовыми маркерами.

Так как изолинии и изополя могут выводиться и для пространственных схем, то перед их выводом выполняется операция удаления невидимых линий, которая для больших схем может занимать достаточно много времени.  Значительно быстрее эта операция выполняется для небольших фрагментов схемы.

                Если на фоне эпюр усилий, изолиний или изополей перемещений и напряжений необходимо вывести еще и значения анализируемого фактора, то следует воспользоваться кнопкой фильтров

 – Оцифровка изополей и изолиний. После нажатия на эту кнопку на схеме появляются значения исследуемого фактора: для эпюр усилий – максимальное значение усилия, для перемещений – значение в узлах схемы, а для напряжений – значения в узлах и в центрах конечных элементов (в зависимости от установок в меню Опции

раздела Настройка графической среды). Для изменения шрифта, цвета и размеров цифр используется функция Установка экранных шрифтов в меню Опции.

Загружения

                При определении РСУ учитываются логические связи между загружениями, которые отражают физический смысл загружений и требования, регламентируемые различными нормативными документами.

                Выделяются три типа загружений:

– независимые (собственный вес, вес оборудования и т.п.);

– взаимоисключающие (ветер слева и ветер справа, сейсмическое воздействие вдоль разных осей координат и т.п.);

– сопутствующие (тормозные при наличии вертикальных крановых нагрузок и т.п.).

                Предоставляется также возможность обозначить знакопеременность загружения при одинаковом модуле его вектора.

* Пискунов В.Г., Федоренко Ю.М. Динамический метод контроля состояния слоистых плит на упругом основании. Архитектура и строительство Беларуси, №5-6, 1994, с.19-22

[1]

            

Полезно заметить, что при вставке между узлами n и n+1 стержня с очень малой жесткостью, потеря обусловленности не происходит [25].

* Проблема перехода от конструкции к расчетной схеме и обратно - от расчетной схемы к конструкции подробно обсуждается в прекрасной книге В.И.Феодосьева [28], которую мы настоятельно рекомендуем всем расчетчикам. Поучительные и тонкие соображения, относящиеся к этому же вопросу содержатся и в монографии И.И.Блехмана, А.Д.Мышкиса и Я.Г.Пановко [1].

---

---